动手学深度学习

1 引言

2 预备知识

2-1 数据操作

N 维数组又称为张量(tensor),与 Numpy 中 ndarray 类似,但相较于 ndarray 多了一些功能:支持 GPU 加速,支持自动微分
0-D:标量:一个类别
1-D:向量:一个特征向量
2-D:矩阵:一个样本,特征矩阵
3-D:一张 RGB 图像(W x H x C)
4-D:一个 RGB 图片批量(B x W x H x C)
5-D:一个视频批量(B x T x W x H x C)

2-1-1 入门

使用 arange 创建一个行向量,需要指定张量的大小,一般 tensor 都存在 CPU 中,并基于 CPU 计算

可以使用 tensor 的属性 shape 访问张量的形状
可以使用 tensor 的属性 numel 访问张量的大小

改变 tensor 的大小,而不改变元素的数量和元素值,可以使用 reshape 函数,其中可以使用-1 来自动计算某一维度的大小

全 0 tensor torch.Zeros(size)

全 1 tensor torch.Ones(size)

随机采样 tenor torch.randn(size),均值为 0,标准差为 1 的标准正态分布
可以自己赋值 tensor torch.Tensor([[1,2,3,4],[1,3,5,6|1,2,3,4],[1,3,5,6]])

访问元素

访问一个元素A[1,2]
访问一行元素A[1,:]
访问一列元素A[:,1]
访问一个区间的元素A[1:3,1:]前闭后开
跳跃访问A[::3,::2] 隔三行,隔两列(第0行,第3行)

2-1-2 运算符

常见的标准算术运算符（+、-、*、/ 和 **）都可以被升级为按元素运算

连接:torch.cat(tensor, dim),如果 dim=0,则是竖着拼接,如果 dim = 1,则是横着拼接

注意:torch.arange(st, en, 类型) 生成一个一维的前闭后开的 int 的 tensor, torch.range(st, en),生成一个 float 的 tensor,闭区间

逻辑运算符构建二元张量。以 X == Y 为例：对于每个位置，如果 X 和 Y 在该位置相等，则新张量中相应项的值为1。这意味着逻辑语句 X == Y 在该位置处为真，否则该位置为0

对张量中的所有元素进行求和，会产生一个单元素张量 X.sum()

2-1-3 广播机制

当进行运算的两个元素之间的维度是不一样的,可以通过适当的赋值行和列进行,一般是沿着数组长度为 1 的轴进行广播

一些操作可能导致新结果分配内存,因此当规模比较大的向量尽量最好原地执行
$Z [:] = X + Y$ 或者 $X = X + Y$

numpy 可以转为 tensor,张量也可以转标量

A = X.numpy() # np.ndarray
B = torch.tensor(A) # torch.tensor

a = torch.tensor([3.5])
a, a.item()   # tensor([3.5]), 3.5

2-2 数据预处理

2-2-1 读取数据集

# 将数据写入文件
import os

os.makedirs((os.path.join('..', 'data')), exist_ok= True)

data_file = os.path.join('..', 'data', 'house_tiny.csv')

with open(data_file, 'w') as f:

    f.write('NumRooms,Alley,Price\n')  # 列名

    f.write('NA,Pave,127500\n')  # 每行表示一个数据样本

    f.write('2,NA,106000\n')

    f.write('4,NA,178100\n')

    f.write('NA,NA,140000\n')

# 使用pandas读取数据

import pandas as pd
data = pd.read_csv("../data/house_tiny.csv")
print(data)

处理缺失数据，典型的方法包括，插值和删除

inputs, outputs = data.iloc[:, 0:2], data.iloc[:, 2] #iloc是指定索引位置
inputs['NumRooms'] = inputs['NumRooms'].fillna(inputs['NumRooms'].mean()) # 当数据是数值的时候,可以用平均值填充

当数据类型是类别值或者离散值的时候，可以采用One-hot的方式进行处理

# get_dummies 是利用pandas实现one hot encode的方式,将类别转为Bool值
inputs = pd.get_dummies(inputs, dummy_na=True) #

然后将其进行转为tensor

# 在转化之前,可以进行np的类型转化,是指object->tensor支持的类型(int, float)
inputs = inputs.astype(float)
torch.tensor(np.ndarry)

2-3 线性代数

2-3-1 标量

仅包含一个数值的,称为标量

x = torch.tensor(2.0)
# 长度是x的绝对

2-3-2 向量

向量是标量组成的列表,这些标量的值称为向量的元素(element)或者分量(component)

x = torch.arange(4)

向量的长度称为向量的维度(dimension),即向量是由多少个元素组成

len(x) or x.shape

2-3-3 矩阵

标量是1x1, 向量是1 x N, 矩阵式M x N
范数： $c = A \cdot b$ hence $| | c | | \leq | | A | | \cdot | | b | |$
矩阵范数: 最小的满足上面公示的值
Frobenius范数: 累积平方和再开根号

特殊矩阵
对称: $A_{i j} = A_{j i}$ , 反对称: $A_{i j} = - A_{j i}$
正定矩阵: $| | x | |^{2} = x^{T} x \geq 0$ generalizes to $x^{T} A x \geq 0$
正交矩阵: 所有行都正交, 所有行都有单位长度, 都可写成 $U^{T} U = 1$

特征向量
不被矩阵改变方向的向量 $A x = λ x$

代码实现

A = torch.arange(20).reshape((5, 4))
# 转置
A.T
# 重新赋值一次A
A=[]
B = A.clone()
# 两个矩阵按元素乘法 
A * B
# 计算其元素的和
x.sum()
# 按指定轴求和
A.sum_axis0 = A.sum(axis = 0) # 维数会减少相应的维度
# 求均值,也可指定相应的维度
A.mean(), A.sum() / A.numel()
# 按某个轴累加求和
A, A.cumsum(axis = 1)
# 向量的点积
x = torch.arange(5, dtype=float).reshape((5))
y = torch.arange(5, dtype=float).reshape((5))
x, y, torch.dot(x, y)
# 矩阵向量积
x = torch.arange(10, dtype=float).reshape((5, 2))
y = torch.arange(2, dtype=float).reshape((2))
x, y, torch.mv(x, y)
# 矩阵乘法
x = torch.arange(10, dtype=float).reshape((5, 2))
y = torch.arange(10, dtype=float).reshape((2, 5))
x, y, torch.mm(x, y)
# 范数
u = torch.norm(x)
# L1范数
u = x.abs().sum()
# 矩阵的F范数
v = torch.norm(torch.ones(4, 9)) # 先拉直再求L2

2-3-4 微积分

亚导数：
将导数扩展到不可微导数，如 y = |x|，在 x=0 处不可导，因此在此处的导数为 $[- 1, 1]$
梯度：
将导数扩展到向量范围

	x(标量)	X(列向量)
y(标量)	标量	行向量
Y(列向量)	列向量	矩阵

2-3-5 自动求导

计算图:(链式法则)
将代码分解为操作子, 将计算表示为一个无环图
自动求导有两种模式:

正向累积
- 首先计算第一项对开始的求导,再计算第二项对第一项的求导...最后一项对倒数第二项求导
- 计算复杂度是 O(n), 内存复杂度是 O(n)(需要存一下前面的结果)
反向传播
- 首先计算最后一项对倒数第二项求导...最后计算第一项对开始的求导
- 计算复杂度是 O(n), 内存复杂度是 O(1)
  显示计算和隐式计算
显示计算是先给公式再给值
隐式计算是先给值再给公式
- 显示构造：把整个计算图都先设计完成，然后再给值
- 隐式构造：就直接写程序流程，然后框架会在后台进行计算图的构建

代码实现

import torch
# 指明需要计算和保存梯度
x = torch.arange(4.0, requires_grad=True) 
x.grad # 获取x的梯度
# 定义y
y = 2 * <x, x>
# 通过y.backward求得y对x的导数
y.backward()
x.grad # 获取x的梯度

# 默认情况下pytorch会累积梯度, 因此计算新梯度的时候,需要清除原有的梯度
x.grad.zero()
y = x.sum()
y.backward()
x.grad

# 对非标量调用backward需要传入一个gradient参数
x.grad.zero_()
y = x * x
y.sum().backward()
x.grad

# 将某些计算移动到记录的计算图以外

x.grad.zero_()
y = x * x
u = y.detach()
z = u * x
z.sum().backward()
x.grad == u  # tensor([True, True, True, True])

x.grad.zero_()
y.sum().backward()
x.grad == 2 * x # tensor([True, True, True, True])

# 分离y来返回一个新变量u，该变量与y具有相同的值， 但丢弃计算图中如何计算y的任何信息。 换句话说，梯度不会向后流经u到x。 因此，下面的反向传播函数计算z=u*x关于x的偏导数，同时将u作为常数处理， 而不是z=x*x*x关于x的偏导数。

3 线性神经网络

3-1 线性回归

线性回归基于几个假设：自变量x和因变量y的关系是线性的，即y可以表示为x的加权和；其次是噪声都比较正常，遵循正态分布

泛化：能够找到一组参数，使得这组参数能够在我们从未见过的数据上实现较低的损失

3-1-1 基本用法

yield 用法：
yield 用法与 return 类似，都是返回值，但是当代码中含有 yield，函数会返回之后的值，然后停止执行，直到使用 next 或者 send 或者再次调用后，继续执行（好处在于，空间少），每次拿到一个数据

def foo(num):
    print("starting...")
    while num<10:
        num=num+1
        yield num
for n in foo(0):
    print(n)

##
starting...   
1   
2  
3   
##

3-2 线性回归的从 0 开始

生成数据集：
首先定义一个正确的函数表达式，利用该表达式生成一些数据，然后加上一些随机噪声

读取数据集
训练模型时要对数据集进行遍历，每次抽取一小批量样本，并使用它们来更新我们的模

3-3 线性回归的简洁实现

使用 torch.nn 模块实现
步骤：

定义 dataset 和 Dataloader
看情况
定义 module
- 重写 init 和 forward 函数
定义 loss
定义优化器 optim
训练
- 获取数据
- 送入网络 net(input)
- 反向传播 loss.backward()
- 优化器更新 optim.Step()
- 一个批次结束，打印一次 loss
  问题
  样本不是批量的整数倍，需要剔除多余的样本吗？
有多少取多少
直接剔除
从下一个 epoch 中补全

3-4 Softmax 回归

独热编码（one-hot encoding）
独热编码是一个向量，他的分量和类别一样多，类别对应分量设置为 1，其他分量都设置为 0。

网络架构
为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。为了解决线性模型的分类问题，我们需要和输出一样多的仿射函数。
用神经网络来表示，softmax 回归也是一个单层神经网络，也是全连接层

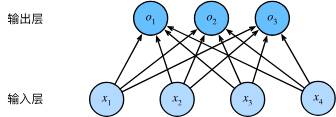
具体来说，对于任何具有 d 个输入和 q 个输出的全连接层，参数开销为 O(dq)

Softmax 运算
要将输出视为概率，我们必须保证在任何数据上的输出都是非负的且总和为1。此外，我们需要一个训练的目标函数，来激励模型精准地估计概率。
softmax 函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持可导的性质，为了完成这一目标，我们首先对每个未规范化的预测求幂，这样可以确保输出非负。为了确保最终输出的概率值总和为1，我们再让每个求幂后的结果除以它们的总和

\hat{y} = s o f t m a x (o), {\hat{y}}_{j} = \frac{e^{o_{j}}}{\sum e^{o_{k}}}

尽管 softmax 是一个非线性函数，但 softmax 回归的输出仍然由输入特征的仿射变换决定。因此，softmax 回归是一个线性模型

对数似然
softmax 函数给出了一个向量 $\hat{y}$ ，我们可以将其视为“对给定任意输入 x 的每个类的条件概率”,假设数据集有{X，Y}个样本，其中索引 i 的样本由其特征向量 x 和独热编码 y 组成，将估计值与实际值比较

P (Y ∣ X) = \prod_{i = 1}^{n} (y^{(i)} ∣ x^{(i)}) .

根据最大似然估计，最大化 P，也就是最小化负对数似然：

- \log P (Y ∣ X) = \sum_{i = 1}^{n} - \log P (y^{(i)} ∣ x^{(i)}) = \sum_{i = 1}^{n} l (y^{(i)}, {\hat{y}}^{(i)})

$\hat{y}$ 和 $y$ 的损失函数为：（交叉熵损失函数）

l (y, \hat{y}) = - \sum_{j = 1}^{q} y_{j} \log {\hat{y}}_{j} .

y 是一个长度为 q 的独热编码向量，所以除了一个项以外的所有项 j 都消失了。由于所有 ${\hat{y}}_{j}$ 都是预测的概率，所以它们的对数永远不会大于 0。因此，如果正确地预测实际标签，即如果实际标签 P(y|x)=1，则损失函数不能进一步最小化,所以，最后结果为所属类别对应的 $\hat{y}$ 的负对数

导数为：

\partial_{o_{j}} l (y, \hat{y}) = \frac{\exp (o_{j})}{\sum_{k = 1}^{q} \exp (o_{k})} - y_{j} = softmax (o)_{j} - y_{j} .

信息论基础
分布 P 的熵：
$H [P] = \sum_{j} - P (j) \log P (j) .$

3-5 图像分类数据集

使用 FashionMNIST 数据集，每个输入图像的高度和宽度均为28像素。数据集由灰度图像组成，其通道数为1
利用 torchvision 得到的数据，是一个元组，访问第一个图片应该是 train_dataset[0][0]

3-6 从 0 开始实现 Softmax 函数

sum 运算符如何沿着张量中的特定维度工作，（同一列（轴0）或同一行（轴1））使用 keepdim = True 或者 false

回想一下，实现 softmax 由三个步骤组成：

对每个项求幂（使用exp）；
对每一行求和（小批量中每个样本是一行），得到每个样本的规范化常数；
将每一行除以其规范化常数，确保结果的和为 1。

交叉熵采用真实标签的预测概率的负对数似然。这里我们不使用 Python 的 for 循环迭代预测（这往往是低效的），而是通过一个运算符选择所有元素。下面，我们创建一个数据样本 y_hat，其中包含2个样本在3个类别的预测概率，以及它们对应的标签 y。有了 y，我们知道在第一个样本中，第一类是正确的预测；而在第二个样本中，第三类是正确的预测。然后使用 y 作为 y_hat 中概率的索引，我们选择第一个样本中第一个类的概率和第二个样本中第三个类的概率。

y = [0, 2]
y_hat[[0, 1], y]表示[y_hat[0][0], y_hat[1, 2]]

tensor.argmax(axis=1) 选出一行中最大元素的小标
cross_entroy 损失函数中包含了 softmax 函数

问答
softlabel 训练策略

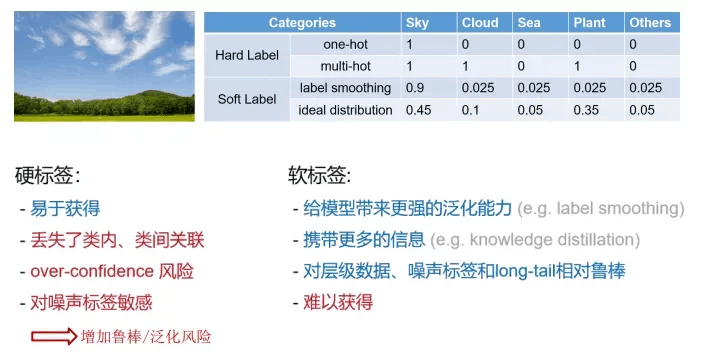
softmax 回归和 logistics 回归分析：
Logistics 是二分类，softmax 多回归

ordinal regression 问题
Ordinal Regression 就是解决类别之间有某种顺序关系的模型，比如年龄，收入等。使模型除了考虑分类损失以外，还要考虑不同类别之间的顺序关系，使与真实标签排序更近的误判的损失小于远离真实标签的误判的损失。介于回归和分类之间的问题

4 多层感知机

4-1 感知机理论

4-1-1 隐藏层

如果不含有隐藏层，只包含一层线性层，就是假设模型是线性的，实际上是不太现实、
在第三章使用线性假设进行图像分类，即区分猫和狗的唯一要求是评估单个像素的强度，这是不合理的，因为任何像素的重要性都以复杂的方式取决于该像素的上下文（周围像素的值）

添加隐藏层
在神经网络中，加入一个或者多个隐藏层来客服线性模型的限制，使其能处理更普遍的函数关系类型，最简单的是，将多个全连接层堆叠在一起，每一层都输出到上面的层，直到生成最后的输出，称为多层感知机（MLP）

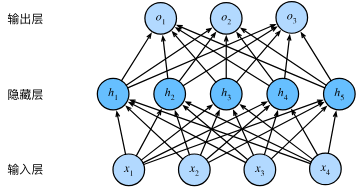
如果仅包括多个线性层，还可以等效为从输入到输出的仿射变换，为了发挥多层架构的潜力，对每个隐藏单元应用非线性的激活函数(activation function), σ()

o = σ (< w, x > + b)

激活函数既可以按行操作,也可以按元素操作,为了构建更通用的多层感知机，我们可以继续堆叠这样的已经使用激活函数的隐藏层

通用近似定理:
一个包含足够多隐含层神经元的多层前馈网络，能以任意精度逼近任意预定的连续函数

4-1-2 激活函数

ReLU 函数(Retified Linear Unit)

R e L U (x) = m a x (x, 0)

当输入为负时，ReLU 函数的导数为0，而当输入为正时，ReLU 函数的导数为1。注意，当输入值精确等于0时，ReLU 函数不可导。在此时，我们默认使用左侧的导数，即当输入为0时导数为0
Tips
在 pytorch 中,只可以进行标量(scalar)对向量(tensor)求导, 如果出现向量对向量求导, 就使用y.backward(torch.ones_like(x), retain_graph=True)
一些变体:参数 ReLU

Sigmoid 函数
对于在 R 上的输入, sigmoid 函数_将输入变换为区间(0, 1)上的输出,sigmoid 通常称为挤压函数

S i g m o i d (x) = \frac{1}{1 + e^{- x}}

导数是 sigmoid(x)(1 - sigmoid(x))

tanh 函数
anh(双曲正切)函数也能将其输入压缩转换到区间(-1, 1)上

t a n h (x) = \frac{1 - e^{- 2 x}}{1 + e^{- 2 x}}

问答
神经网络的一层:
是指一层神经元和非线性变换
ReLU 函数：
是分段线性函数，总体来看不是线性，激活函数的本质是引入非线性，一般用 ReLU 即可
怎么根据输入数据，确定较好的深度和宽度
逐步加深，每次选择较好的一个隐藏层的神经元个数，在此基础上继续加深

4-2 模型选择

训练模型是为了发现数据存在的模式，而不是记住数据
过拟合： 将模型在训练数据上拟合的比在潜在分布中更接近的现象称为过拟合，测试集要低
训练误差： 在训练数据集上得到的误差
泛化误差： 模型应用在同样从原始样本的分布中抽取的无限多数据样本（可用测试集代替）时，模型误差的期望

4-2-1 统计学习理论

独立同分布假设：训练数据和测试数据都是从相同的分布中独立提取的

4-2-2 模型复杂性

一条简单的经验法则相当有用：统计学家认为，能够轻松解释任意事实的模型是复杂的，而表达能力有限但仍能很好地解释数据的模型可能更有现实用途
影响模型泛化的因素：

可调整参数的数量：当自由度很大时，模型往往过拟合
参数采用的值：权重的取值范围过大时，也会过拟合
训练样本的数量：样本数量过少，容易过拟合
如果输入特征为 d，隐藏层神经元为 m，最后输出为 d，则需要的参数量为
（d+1）* m+（m+1 ）* k

4-2-3 验证集

为了确定超参数，需要使用一些数据来进行测试衡量，如果使用测试集，有可能导致测试数据的过拟合，因此不能依靠测试数据进行模型选择。然而，我们也不能仅仅依靠训练数据来选择模型。解决此问题的常见做法是将我们的数据分成三份，除了训练和测试数据集之外，还增加一个验证数据集（validation dataset）

4-2-4 K 折交叉验证

提出缘由：当训练数据过少时，可能无法提供合适的验证集
方法：将数据分成 K 个不相交的子集，执行 K 次模型的训练与验证，每次在 K-1 个子集上进行训练，并在剩余的 1 个子集上进行验证（在该轮训练过程中没有用到）
for i = 1...k
使用第 i 块作为验证数据集，其余作为训练数据集
报告 K 个验证集误差的平均

4-2-5 过拟合和欠拟合

欠拟合：训练误差和泛化误差都很大(偏差很大)
过拟合：训练误差小，泛化误差大（偏差小，方差大）

VC 维
VC Dimension：全称是 Vapnik-Chervonenkis dimension。其用来衡量一个模型的复杂度，定义为：在该模型对应的空间中随机撒 x 点，然后对其中的每个点随机分配一个2类标签，使用你的模型来分类，并且要分对，请问 x 至多是多少。这个 x 就是 VC 维。
二维线性模型的 VC 维是 3，支持 N 维的感知机是 N+1

4-2-6 问答

SVM 的缺点：
对于大规模数据集计算难度很高
可调性不高
在 validation dataset 上调整参数，查看是否 overfitting 和 underfitting
如何有效设计超参数
超参数的设计靠经验，如何搜索？自己调整，或者随机选取
如果出现样本类别不平衡，该如何做？
如果真实样本分布也是这样，可以不做处理，如果真实样本分布是平衡的，可以给小数据样本进行加权处理
如果样本数量很大，都可以
如果样本数量不大，可以按照两种样本数差不多的方式划分
K 折交叉验证第一次划分为 K 个分组以后，之后就不再进行随机划分

4-3 权重衰退

权重衰减（weight decay）又称 L2 正则化，这项技术通过函数与零的距离来衡量函数的复杂度，一种简单的方法是通过线性函数的权重向量来度量其复杂性，如 $∣∣ w ∣ ∣^{2}$ 。要保证权重向量比较小，最常用的方法是将其范数作为惩罚项加到最小化损失的问题中，将原来的训练目标最小化训练标签上的预测损失调整为最小化预测损失和惩罚项损失之和，同时引入正则化常数λ来进行权重的平衡
L2 正则化线性模型构成经典的岭回归算法，而 L1 正则化线性回归是统计学中类似的基本模型，通常称为套索回归。使用 L2 范数的一个原因是它对权重向量的大分量施加巨大惩罚，这使得我们的学习算法偏向于在大量特征上均匀分布权重的模型
一般不对偏置进行正则

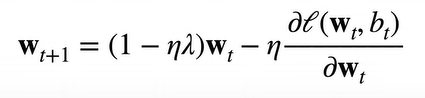
在梯度下降时，首先是对 w 进行减小，所以称为权重衰退
λ一般取 0.001， 0.0001

4-4 Dropout

使用有噪音的数据相当于 Tikhonov 正则

在前向传播的过程中，计算每一内部层的同时注入噪声，从表面看是在训练过程中丢弃了一些神经元，在整个训练过程的每一次迭代过程中，dropout 在计算下一层之前将当前层中的一些节点置零

在 dropout 中，通过按保留的节点的分数进行规范化来消除每一层的偏差，也就是每个中间节点的激活值 h 以暂退概率 p 由随机变量 p‘替换，如下所示：

x_{i}^{'} = {\begin{cases} 0 & with probablity p \\ \frac{x_{i}}{1 - p} & otherise \end{cases}

保证了期望值不变

E [x_{i}] = p \cdot 0 + (1 - p) \frac{x_{i}}{1 - p} = x_{i}

正则项只在训练中使用：会影响模型参数的更新
在推理过程中，丢弃法直接返回输入 h=dropout(h)

问答
dropout 随机置零对求梯度和反向传播的影响？
使得丢弃处的位置梯度为 0

CUDNN 每次运算结果不一样，这是因为并行时候的矩阵运算顺序不一样的原因

丢弃法是在训练过程中把神经元丢弃后训练，在预测时网络中的神经元没有丢弃，直接返回输入，不会进行处理

BN 是给卷积层用的，Dropout 是给全连接层用的

4-5 前向传播、反向传播和计算图

4-5-1 前向传播

前向传播（forward propagation）是指按顺序（从输入层到输出层）计算和存储网络中每层的结果
输入是 $x$ ，经过第一个隐藏层后为 $z = W^{(1)} x$ , 经过激活函数后为 $h = ϕ (z)$ ，输入到第二层隐藏层后得到 $o = W^{(2)} h$ ，损失函数为 $l$ ，可以计算得到单个样本的损失为 $l = l o s s (o, y)$ ，根据正则化的定义，给定超参数λ，正则化项为 $s = \frac{λ}{2} (∣∣ w^{1} ∣ ∣^{2} + ∣∣ w^{(2)} ∣ ∣^{2})$ ，最后的损失为 $J = l + s$

前向传播计算图：方块表示变量，圆圈表示运算

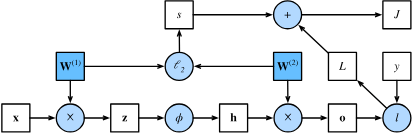
4-5-2 反向传播

反向传播（back propagation）是指计算神经网络参数梯度的方法，根据链式规则，按相反的方向（从输出到输入）遍历网络。该方法存储了计算梯度的中间变量
!http://cdn.zghhui.me/img/Pasted image 20231124170505.png

4-6 让训练更加稳定

假定如下网络 $$\mathbf{h}^{(l)} = f_l (\mathbf{h}^{(l-1)}) \text{ 因此 } \mathbf{o} = f_L \circ \ldots \circ f_1(\mathbf{x}).$$
任何一组参数的导数为：

\partial_{W^{(l)}} o = \underset{M^{(L)} \overset{def}{=}}{\underset{⏟}{\partial_{h^{(L - 1)}} h^{(L)}}} \cdot \dots \cdot \underset{M^{(l + 1)} \overset{def}{=}}{\underset{⏟}{\partial_{h^{(l)}} h^{(l + 1)}}} \underset{v^{(l)} \overset{def}{=}}{\underset{⏟}{\partial_{W^{(l)}} h^{(l)}}} .

梯度是一系列矩阵的乘积，很容易出现过大或者过小

梯度爆炸：
ReLU 作为激活函数
值超出范围，对 16 位浮点数尤为严重
学习率过于敏感

梯度消失：
Sigmoid 作为激活函数
梯度值变为 0，对 16 位浮点数尤为严重，不管如何选择学习率，训练没有进展，对网络的底部（靠近输入的地方）

对称性：
如果将隐藏层所有参数都初始化为 W=c，在这种情况下，在前向传播的过程中，这些隐藏单元采用相同的输入和参数，产生相同的激活，该激活被输送到输出单元，在反向传播过程中，会产生相同的梯度，这样的迭代永远不会打破对称性，但暂退法正则化可以

保持稳定性的方法:
目的是让梯度值在合理的范围内(1e-6, 1e3)
将乘法变成加法 ResNet 和 LSTM
归一化: 梯度归一化和梯度裁剪
合理的权重初始化和激活函数

4-6-1 参数初始化

使用正态分布来初始化权重，或者默认的随机初始化
Xavier 初始化
（不考虑激活）权重( $δ^{2}$ )和参数 ( $γ^{2}$ ) 都假定有各自独立的均值（0）和方差，则输出也会有相应的方差

\begin{array}{r} \begin{aligned} E [o_{i}] & = \sum_{j = 1}^{n_{in}} E [w_{i j} x_{j}] \\ = \sum_{j = 1}^{n_{in}} E [w_{i j}] E [x_{j}] \\ = 0, \\ Var [o_{i}] & = E [o_{i}^{2}] - (E [o_{i}])^{2} \\ = \sum_{j = 1}^{n_{in}} E [w_{i j}^{2} x_{j}^{2}] - \sum_{j \neq k} w_{i, j}^{t} w_{i, k}^{t} h_{j}^{t - 1} h_{k}^{t - 1} (= 0) \\ = \sum_{j = 1}^{n_{in}} E [w_{i j}^{2}] E [x_{j}^{2}] \\ = n_{in} σ^{2} γ^{2} . \end{aligned} \end{array}

保持经过神经元的输入数据和输出数据的方差（ $γ^{2}$ ）不变的方法可以是设置 $n_{in} σ^{2} = 1$
既考虑前向传播 $n_{i n}$ 和反向传播 $n_{o u t}$ , 虽然无法同时满足，但可以

\begin{array}{r} \frac{1}{2} (n_{in} + n_{out}) σ^{2} = 1 或等价于 σ = \sqrt{\frac{2}{n_{in} + n_{out}}} . \end{array}

这是现在标准且实用的_Xavier 初始化_的基础
正态分布和均匀分布的初始化分别为：

\begin{aligned} N (0, \sqrt{2 / (n_{t - 1} + n_{t})}) \\ U (- \sqrt{6 / (n_{t - 1} + n_{t})}, \sqrt{6 / (n_{t - 1} + n_{t})}) \end{aligned}

考虑激活（线性激活时）

o (x) = a x + b

保持经过神经元的输入数据和输出数据的方差（ $γ^{2}$ ）不变的方法是使得 $a^{2} = 1$
使用泰勒展开分析每个激活函数：
对于 tanh 和 ReLU 激活函数使用激活函数展开后，在原点处 x 的系数满足条件
对于 sigmoid 函数需要进行一定的调整，4sigmoid - 2

问答
nan 一般是除 0； inf 是超限，可能是学习率太大
梯度消失不仅仅是由 sigmoid 函数引起
对于有多路不同输入的（比如经过两个网络），可以对不同网络设置权重来处理

5 深度学习计算

5-1 层和块

整个深度学习模型的架构：接收输入，产生输出，包含一组参数。其中每个单独的层也是接收输入，产生输出，包含一组参数。块（block） 可以描述单个层、由多个层组成的组件或整个模型本身，使用块进行抽象的一个好处是可以将一些块组合成更大的组件，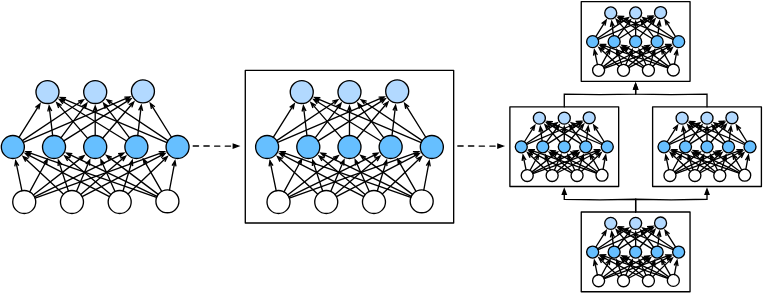
多个层被组成块，块又形成更大的模型
从编程的角度来看，块由类（class）表示，他的任何子类都必须定义一个将其输入转为输出的前向传播函数，必须存储必要的参数，为了计算梯度，块必须具有反向传播函数。

5-1-1 自定义块

块的基本功能：

将输入数据作为其前向传播函数的参数
通过前向传播生成输出
计算其输出关于输入的梯度，通过反向传播完成
存储和访问前向传播的所需的参数
初始化模型参数

5-1-2 顺序块

重写 Sequential 类，其中 Sequential 类是为了把其他模块串起来，主要实现两个关键函数：

一种将块逐个追加到列表中的函数
一种前向传播函数，用于将输入按追加块的顺序传递给块组成的“链条”

class MySequential(nn.Module):
    def __init__(self, *args):
        super().__init__()
        for idx, module in enumerate(args):
            # 这里，module是Module子类的一个实例。我们把它保存在'Module'类的成员
            # 变量_modules中。_module的类型是OrderedDict
            self._modules[str(idx)] = module

    def forward(self, X):
        # OrderedDict保证了按照成员添加的顺序遍历它们
        for block in self._modules.values():
            X = block(X)
        return X

注：
enumerate() 函数用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标，一般用在 for 循环当中。
_modules 是一个字典

当需要某个参数不需要进行更新时（常数参数），可以将其 requires_grad=False，在 forward 函数中也可以加一些可执行的代码

5-2 参数管理

5-2-1 参数访问

当通过 Sequential 类定义模型时，我们可以通过索引来访问模型的任意层。这就像模型是一个列表一样，每层的参数都在其属性中。如下所示，我们可以检查第二个全连接层的参数

print(net[2].state_dict())

OrderedDict([('weight', tensor([[-0.0427, -0.2939, -0.1894,  0.0220, -0.1709, -0.1522, -0.0334, -0.2263]])), ('bias', tensor([0.0887]))])

参数是复合的对象，包含值、梯度和其他额外的信息
访问某一层的权重

cov2d.weight.data

5-2-2 一次性访问所有参数

print(*[(name, param.shape) for name, param in net[0].named_parameters()])
print(*[(name, param.shape) for name, param in net.named_parameters()])

net.state_dict()['2.bias'].data

嵌套块

def block1():
    return nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                         nn.Linear(8, 4), nn.ReLU())

def block2():
    net = nn.Sequential()
    for i in range(4):
        # 在这里嵌套
        net.add_module(f'block {i}', block1())
    return net

rgnet = nn.Sequential(block2(), nn.Linear(4, 1))
rgnet(X)

因为层是分层嵌套的，所以我们也可以像通过嵌套列表索引一样访问它们。下面，我们访问第一个主要的块中、第二个子块的第一层的偏置项。rgnet[0][1][0].bias.data

5-2-3 参数初始化

默认情况下，PyTorch 会根据一个范围均匀地初始化权重和偏置矩阵，这个范围是根据输入和输出维度计算出的
可以调用内置的初始化器
apply 函数会对网络中所有的层, 扫一遍, 执行对应的初始化

def init_normal(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, mean=0, std=0.01)
        nn.init.zeros_(m.bias)
net.apply(init_normal)

也可以对不同的层分别初始化

def init_xavier(m):
    if type(m) == nn.Linear:
        nn.init.xavier_uniform_(m.weight)
def init_42(m):
    if type(m) == nn.Linear:
        nn.init.constant_(m.weight, 42)

net[0].apply(init_xavier)
net[2].apply(init_42)
print(net[0].weight.data[0])
print(net[2].weight.data)

也可以自定义初始化 D2L 自定义初始化
注意，我们始终可以直接设置参数。

5-2-4 参数绑定

# 我们需要给共享层一个名称，以便可以引用它的参数
shared = nn.Linear(8, 8)
net = nn.Sequential(nn.Linear(4, 8), nn.ReLU(),
                    shared, nn.ReLU(),
                    shared, nn.ReLU(),
                    nn.Linear(8, 1))

参数绑定后, 不仅值相等，而且由相同的张量表示。因此，如果我们改变其中一个参数，另一个参数也会改变。这里有一个问题：当参数绑定时，梯度会发生什么情况？答案是由于模型参数包含梯度，因此在反向传播期间第二个隐藏层（即第三个神经网络层）和第三个隐藏层（即第五个神经网络层）的梯度会加在一起。

有些函数是带下划线_的, 这表明是原地操作函数(置换函数), 不带下划线的是有返回值

对于自定义的参数, 需要继承 nn.Parameter 类, 在之后的访问中, 可以使用 self.bias.data 访问它的值

创建 tensor 时, size 的位置如果是写(x, )表示创建列向量

5-2-5 读写文件

可以通过 torch.save()保存和 torch.load()加载文件数据
对于模型来说, 可以保存和加载模型的参数:
torch.save(net.state_dict(), 'mlp.params')
如果只保存参数, 加载时需要先声明一个模型, 然后使用 net.load_state_dict(torch.load('xx'))进行加载

问答
将类别变量转为 one-hot 时, 内存爆炸

采用稀疏矩阵存储
对于竞赛时的介绍这一特征, 可以不用把每个人的介绍作为一项, 而是把一个词拿出来作为特征
forward 函数是怎么调用的
对于网络 net 来说, 调用 net(x)就等效于调用了 forward 函数
自定义激活函数一般不用考虑是否可导, 但实际上很难遇到不可导的情况, 如果遇到, 随便给一个数即可

6 卷积神经网络

多层感知机很适合处理表格数据, 其中行对应样本, 列对应特征, 但对于高维特征数据, 缺少结构的网络可能变得不适用
卷积神经网络(convolutional neural network)是机器学习利用自然图像中的一些已知结构的的创造性方法

6-1 从全连接到卷积

6-1-1 不变性

卷积神经网络正是将空间不变性（spatial invariance）的这一概念系统化，从而基于这个模型使用较少的参数来学习有用的表示。

平移不变性: 不管检测对象出现在哪个位置, 神经网络的前面几层应该对相同的图像区域具有相似的反应, 即"平移不变性"
局部性: 神经网络的前面几层应该只探索输入图像的局部区域, 而不过度在意图像间隔较远的区域的关系, 最终可以聚合这些局部特征, 以在整个图像级别进行预测

为什么是四维, 在 MLP 中输入是一维, 输出是一维, 因此 W 是二维(输入, 输出), 现在输入是二维, 输出是二维, 因此 W 是四维

局部性：
为了计算 H 的相关信息，a, b 不应该取得值很大，距离(i, j)很远 ,这意味着 $∣ a ∣> δ$ 和 $∣ b ∣> δ$ 的范围之外, 可以设置 V=0, 重写 H

[H]_{i, j} = u + \sum_{a = - Δ}^{Δ} \sum_{b = - Δ}^{Δ} [V]_{a, b} [X]_{i + a, j + b} .

上式是卷积层, 卷积神经网络是包含卷积层的特殊神经网络, V 称为卷积核或者滤波器, 或者称为该卷积层的权重, 是可学习的参数,
当图像处理的局部区域很小时，卷积神经网络与多层感知机的训练差异可能是巨大的：以前，多层感知机可能需要数十亿个参数来表示网络中的一层，而现在卷积神经网络通常只需要几百个参数，而且不需要改变输入或隐藏表示的维数。参数大幅减少的代价是，我们的特征现在是平移不变的，并且当确定每个隐藏活性值时，每一层只包含局部的信息。以上所有的权重学习都将依赖于归纳偏置。当这种偏置与现实相符时，我们就能得到样本有效的模型，并且这些模型能很好地泛化到未知数据中。但如果这偏置与现实不符时，比如当图像不满足平移不变时，我们的模型可能难以拟合我们的训练数据。

6-1-2 卷积

数学中的卷积是:

(f * g) (x) = \int f (z) g (x - z) d z

卷积是把一个函数翻转, 并移位 x, 测量 f 和 g 的重叠, 当为离散的对象时, 积分就变为求和

(f * g) (i, j) = \sum_{a} \sum_{b} f (a, b) g (i - a, j - b) .

这与上上式很相似, 但有个正负的区别

6-1-3 通道

图像一般是三个通道, 即图像是长度, 宽度, 颜色组成的三维张量, 因此卷积核 V 也应该变成三维, 同时隐式表示也变为具有一系列通道的二维张量(三维), 这些通道有时称为特征映射, 因为每个通道都向后续层提供一组空间化的学习特征

[H]_{i, j, d} = \sum_{a = - Δ}^{Δ} \sum_{b = - Δ}^{Δ} \sum_{c} [V]_{a, b, c, d} [X]_{i + a, j + b, c},

此时 V 是四维, d 表示通道, c 表示像素的多维表示

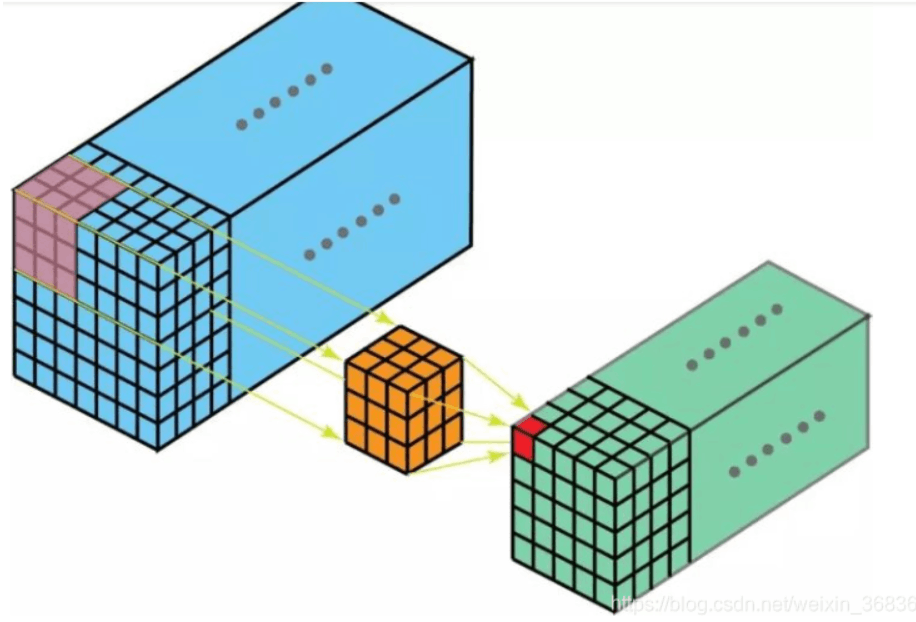
6-2 图像卷积

6-2-1 互相关和卷积:

互相关：计算表达式中是正号
卷积：计算表达式中是负号
卷积层实际上做的是互相关

卷积窗口从输入张量的左上角开始，从左到右、从上到下滑动。当卷积窗口滑动到新一个位置时，包含在该窗口中的部分张量与卷积核张量进行按元素相乘，得到的张量再求和得到一个单一的标量值

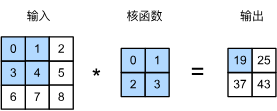
输入大小是 $n_{h} \times n_{w}$ , 卷积核大小是 $k_{h} \times h_{w}$ , 则输出是 $(n_{h} - k_{h} + 1) \times (n_{w} - k_{w} + 1)$

为了计算卷积, 可以对卷积核进行水平和竖直翻转, 然后与输入数据进行互相关运算, 但为了与深度学习中的文献保持一致, 互相关运算=卷积运算

6-2-2 特征映射和感受野

卷积层有时候称为特征映射
在卷积网络中, 某一层元素 x 的感受野, 指的是在前向传播期间可能影响 x 计算的所有元素(上一层)
对于一个 3x3 的输入, 第一层卷积核大小为(2 x 2), 则输出 Y(2 x 2) 的每一个元素的感受野的大小为 4, Y 经过一个卷积核大小为(2 x 2)的卷积, 输出 Z (1个元素)的感受野包括 Y 的四个元素, 最初输入的 9 个元素
例子: 经过两个 3x3 卷积核的感受野的大小为 5 x 5
因此，当一个特征图中的任意元素需要检测更广区域的输入特征时，可以构建一个更深的网络。

问答
为什么不该看那么远, 感受野不应该是越大越好吗?
是越大越好, 但做一个核很大的, 不如做核小(3 x 3), 但是网络很深的效果好

同时使用两个不同尺寸的 Kernel 进行计算, 然后再计算出一个更加适合的 kernel 从而提高特征提取的性能

平移不变性是体现在无论处理哪些元素, 都是使用一个同样的核

损失随着迭代次数变化图抖动很厉害, 这可能是因为学习率和批量大小的原因, 抖动没关系, 只要下降即可

6-3 填充和步幅

6-3-1 填充

在应用多层卷积时, 常常会丢失边缘像素, 虽然使用的是小卷积核, 对于单个卷积只会丢失几个像素，但随着应用许多连续卷积层，累计丢失的像素就会很多，解决的方法就是填充(padding)
如果添加 Ph 行填充, Pw 列填充(都是一半在顶部, 一半在底部), 则输出的形状为 $(n_{h} - k_{h} + p_{h} + 1) \times (n_{w} - k_{w} + p_{w} + 1)$
许多情况下, 需要设置 $(p_{h} = k_{h} - 1), (p_{w} = k_{w} - 1))$ , 使得经过卷积后的形状不变. 如果卷积核的长度是偶数, 则顶部多一行, 如果是奇数, 上下一样多

选择卷积核的高度和宽度一般是奇数, 这样使得填充是对称和一样的, 同时如果卷积核大小是奇数, 可以按照卷积核中心进行互相关计算

在 pytorch 中的 nn.Conv2d 的参数 padding 中, 默认是 2 倍, 即输入的参数只是填充一边的数即可

当卷积核的高度和宽度不相同时, 可以填充不同的高度和宽度, 如果使用 5x3 卷积, 则应该分别填充 4 和 2, 对应 padding=(2, 1)

6-3-2 步幅

卷积窗口从输入张量的左上角开始，向下、向右滑动, 默认每次滑动一个元素
为了高效计算或者缩减采样次数, 卷积窗口可以跳过中间位置, 每次滑动多个元素, 称每次滑动元素的数量称为步幅(stride)
当垂直步幅为 Sh, 水平步幅为 Sw 时, 输出形状为:

⌊ \frac{n_{h} - k_{h} + p_{h} + s_{h}}{s_{h}} \times \frac{n_{w} - k_{w} + p_{w} + s_{w}}{s_{w}} ⌋

当 $(p_{h} = k_{h} - 1), (p_{w} = k_{w} - 1))$ 时，输出可以简化为：

⌊ \frac{n_{h} - 1 + s_{h}}{s_{h}} \times \frac{n_{w} - 1 + s_{w}}{s_{w}} ⌋

问答
不选步幅为 1 的情况是: 计算量太大,需要很多层来完成

如果需要步幅, 可以将步幅穿插在网络中间

是否有办法让超参数跟这一块训练? Neural Network Architecture Search
但是一般用经典的网络结构即可

通过多层卷积最后输出和输入形状相同,信息是否会丢失呢? 机器学习可以认为会丢失一些信息, 会把像素信息压缩到人能够理解的维度里面, 其中有一些语义信息

6-4 多输入多输出通道

每个 RGB 图像都是具有 3 x h x w 的形状, 其中 3 这个轴就称为通道维度

6-4-1 多输入通道

每个元素都有自己的卷积核
当输入包含多个通道时, 需要构造一个与输入数据具有相同通道数的卷积核, 以便与输入数据进行互相关运算, 即输入数据是(c, h, w) 卷积核也应该是(c, kh, kw)大小
此时进行卷积计算就可以是立方体进行对应求积, 然后再相加

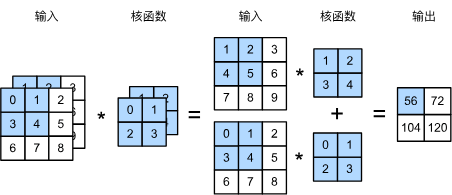
6-4-2 多输出通道

随着神经网络层数的增加, 常会增加输出通道的维数, 通过减少空间分辨率以获得更大的通道深度, 将每个通道看作是对不同特征的响应, 但实际上每个通道不是独立学习的, 而是为了共同使用而优化的
用 ci 和 co 分别表示输入和输出通道, 并让 kh 和 kw 表示卷积核的高度和宽度, 为了获得多个通道的输出, 我们可以为每一个输出通道创建一个形状为(ci, kh, kw)的卷积核, 这样的卷积核的形状是(co, ci, kh, kw), 再计算的时候, 先用(ci, kh, kw)获得一个通道的结果, 再计算 co 次即可

torch.stack([], dim=)
沿着一个新维度对输入张量序列进行连接。序列中所有的张量都应该为相同形状。
浅显说法：把多个 2 维的张量凑成一个 3 维的张量；多个 3 维的凑成一个 4 维的张量…以此类推，也就是在增加新的维度进行堆叠。

torch.cat 和 torch.stack 的区别在于 cat 会增加现有维度的值,可以理解为续接，stack 会新加增加一个维度。

每个输出通道可以识别特定的模式，输入通道核识别并组合输入中的模式

6-4-3 1x1 卷积层

1x1 卷积的实际作用
失去了卷积层特有的能 y 力——在高度和宽度维度上，识别相邻元素间相互作用的能力，1x1 卷积的唯一计算发生在通道上，即不识别空间模式，只是融合通道
输入和输出具有相同的高度和宽度，输出的每个元素都是输入图像中同一位置的元素的线性组合

相当于输入形状为 $h w \times c$ , 权重为 $c_{o} c_{i}$ 的全连接层
每个输入的通道都有一个二维的卷积核，所有通道结果相加得到一个输出通道的结果
每个输出通道都有一个三维的卷积核

二维卷积层
$输入 X : c_{i} \times n_{h} \times n_{w}$
$核 W : c_{o} \times c_{i} \times k_{h} \times k_{w}$
$偏差 B : c_{o} \times c_{i}$
$输出 Y : c_{o} \times m_{h} \times m_{w}$
计算复杂度是 $c_{o} \times c_{i} \times k_{h} \times k_{w} \times m_{h} \times m_{w}$

6-4-2 问答

一般来说，输入和输出的大小没变，输出通道不太会变化，如果输入图像的尺寸减半了，一般输出通道会加倍，这是将空间中的信息放到通道中存储

每个通道的卷积核是不一样的，同一层不同通道的卷积核大小一般一样

如果 RGB 图+深度图，相当于输入是四个通道，需要用到三维卷积

MobileNet：与正常卷积不同，先用 3x3 卷积进行计算，但不进行空间融合求和，然后再用 1x1 卷积层进行空间融合，计算量会小

卷积可以获得位置信息，可以通过池化层来使得卷积不那么获取位置信息

多通道，核之间是不共享参数的

feature map 是输出特征

6-4 池化层

当处理图像的时候，希望逐渐减低隐藏层中的空间分辨率和聚集信息，这样随着再神经网络中层叠的上升，每个神经元对齐敏感的感受野（输入）就越大

机器学习任务往往会跟全局图像的问题有关，所以在最后一层的神经元中，应该对整个输入的全局都比较敏感，通过逐渐聚合信息，生成越来越粗糙的映射，最终实现学习全局表示，将卷积层的所有优势保留在中间层

池化层的目的是：降低卷积层对位置的敏感性，同时降低对空间降采样表示的敏感性
没有可学习的参数

6-4-1 最大池化层和平均池化层

池化层由一个固定形状的窗口组成，该窗口根据其步幅大小在输入的所有区域上滑动，为固定形状窗口（有时称为 池化窗口 ）遍历的每个位置计算一个输出。

池化窗口的形状是 2x2 的池化层，称为 2 x2 池化层，池化操作称为 2x2 池化

6-4-2 填充和步幅

池化层也可以改变输出和性质，通过填充和步幅来获得所需要的形状

pool2d = nn.MaxPool2d((2, 3), stride=(2, 3), padding=(0, 1))
pool2d(X)

pytorch 中步幅默认是池化核的大小

6-4-3 多个通道

在处理多通道输入数据时，池化层是在每个输入通道上单独运算，而不是像卷积层那样在通道上对输入进行汇总，意味着池化层的输入通道和输出通道相同

6-4-4 问答

池化一般是放在卷积后面

池化逐渐用的变少, 一部分是降低敏锐度(由于现在都采用了数据增强), 另一部分是减少计算量(可以在卷积里面用 stride 也可以实现降低计算量)

6-5 卷积神经网络 LeNet

LeNet-5 由两个部分组成,

卷积编码器: 由两个卷积层组成
全连接层密集块: 由三个全连接层组成

每个卷积块中的基本单元是一个卷积层, 一个 sigmoid 激活函数和平均池化层, 每个卷积层使用 5x5 卷积核和一个 sigmoid 激活函数.这些层将输入映射到多个二维特征输出, 通常同时增加通道的数量. 第一层卷积层有六个输出通道, 第二个卷积层有 16 个输出通道, 每个 2x2 池化操作(步幅是 2)通过下采样将维数减少四倍, 卷积的输出形状由批量大小, 通道数, 高度, 宽度决定

为了将卷积块的输出传递给全连接层, 必须在小批量中展平每个样本, 即将这个四维输入转为全连接层所期望的二维输入,

6-5-2 问答

在压缩数据的时候，一般高宽减半，通道加倍，通过增加通道数来提升模式的匹配能力

当图像很大的时候，用 MLP 很难跑，且容易 overfitting

查看网络学到了什么 cnn explanner

7 现代卷积神经网络

7-1 深度卷积神经网络

从对最终模型精度的影响来说，更大或更干净的数据集、或是稍微改进的特征提取，比任何学习算法带来的进步要大得多。

7-1-1 学习表征

特征本身应该被学习，在合理地复杂性前提下，特征应该由多个共同学习的网络层组成，每层都有可学习的参数
在 AlexNet 中，网络的低层学到了一些类似于传统滤波器的特征抽取器，更高层建立在这些底层表示的基础上，以表示更大的特征，而更高层可以检测整个物体，最终的隐藏神经元可以学习图像的综合表示

深度卷积神经网络突破可归因于两个因素：

大规模数据 ImageNet
GPU 硬件支持
GPU 的运算速度快于 CPU 的原因

7-1-2 AlexNet

AlexNet 与 LeNet 很类似，但是有着显著差异：

AlexNet 要深，由 8 层组成，五个卷积层，两个全连接隐藏层和一个全连接输出层
使用 ReLU 作为激活函数

模型设计

第一层采用了 11x11 的卷积层，这是由于 ImageNet 的图像要比 MNIST 中大十倍以上，需要更大的窗口来捕获目标。第二层是 5x5 卷积层，然后是三个 3x3 卷积，在第一层、第三层、第五层卷积之后加入了 3x3，步幅为 2 的最大池化层，且通道数是 LeNet 的十倍
最后一个卷积层后面有两个全连接层，分别有 4096 个输出，这两个大全连接层将近有 1G 的模型参数，因此原版的 AlexNet 采用了双数据流设计，使得每个 GPU 只负责存储和计算模型一半的参数

激活函数
ReLU 激活函数计算简单，且训练更加容易。Sigmoid 函数在输出为 1 和 0 的地方梯度为 0 会出现梯度消失

参数控制和预处理
AlexNet 采用了 Dropout 来控制全连接层的复杂度，而 LeNet 只采用了权重衰减（正则化）同时 AlexNet 还采用了大量的图像增强数据，如翻转、裁切和变色等，使得模型更加健壮，更大的样本量减少了过拟合

7-1-3 问答

AlexNet 最后有两个全连接层，如果去掉一个效果会变差

7-2 VGG

AlexNet 虽然很有效，但是并没有提供一个通用的模板来指导后续的研究人员设计新的网络

7-1-1 VGG 块

经典卷积神经网络的基本组成部分是下面这个序列：

带填充以保持分辨率的卷积层
非线性激活函数 ReLU
池化层
在一个 VGG 块中，由一系列卷积层组成，后面再加上用于空间下采样的最大池化层，在最初的 VGG 论文中，作者使用了 3x3 卷积核，填充为 1（保持尺寸）的卷积层，和带有 2x2 池化窗口，步幅为 2（每个块后的分辨率减半）的最大池化层

7-2-2 VGG 网络

与 AlexNet、LeNet 一样, VGG 网络可以分为两个部分, 第一部分主要是由卷积层和池化层组成, 第二部分主要由全连接层组成

原始的 VGG 网络有五个卷积块, 其中前两个块中各有一个卷积层, 后三个块中包含两个卷积层, 第一个模块中有 64 个输出通道, 后续模块将输出通道翻倍, 直到达到 512, 该网络使用了 8 个卷积和 3 个全连接层, 也成为 VGG-11

7-2-3 问答

为什么训练 loss 一直在下降，但是测试 loss 不降低

过拟合
测试数据集代码写错了

7-3 网络中的网络 NiN

LeNet AlexNet VGG 都有一个共同的特征：通过一系列的卷积层和池化层来提取空间结构特征，然后通过全连接层来对特征的表征进行处理

NiN: 在每个像素的通道上分别使用多层感知机

7-3-1NiN 块

卷积层的输入和输出由四维张量组成，张量的每个轴分别对应样本、通道、高度和宽度。另外，全连接层的输入和输出通常是分别对应于样本和特征的二维张量。
NiN 的想法是，在每个像素位置用一个全连接层，将权重连接到每个空间位置，可以视为 1 x1 卷积，或作为在每个像素位置上独立作用的全连接层。从另一个角度看，将空间维度中的每个像素是为一个样本，通道维数视作不同的特征

NiN 从一个普通的卷积层开始，后面是两个 1x1 卷积层，这两个 1 x1 卷积层充当带有 ReLU 激活函数的逐像素全连接层，第一层的卷积窗口形状通常由用户设置。随后的卷积窗口形状固定为 1x1
NiN 完全取消了全连接层，使用了一个 NiN 块，其输出通道等于标签类别的数量，最后放一个全局平均池化层(每个通道算出一个平均值)，经过 softmax 生成一个对数概率
NiN 的优点是减少了模型所需的参数数量，但是加大了训练时间

7-3-2 问答

softmax 是在 crossentropy 损失函数中

加入全局池化层，使得模型的复杂性降低了，泛化性增强

为什么 NiN 块使用了两个 1x1 卷积块

应该是尝试出来的

NiN 中的 1x1 卷积是对一个像素的不同通道的位置进行全连接

7-4 含并行连结的网络(GoogLeNet)

GoogLeNet 吸收了 NiN 中串联网络的思想, 并在此基础上进行了改进, 这篇论文的重点是解决了什么样的卷积核最合适的问题, 文中的一个观点是有时候使用不同大小的卷积核的组合是有利的

7-4-1 Inception 块

It was arguably also the first network that exhibited a clear distinction among the stem (data ingest), body (data processing), and head (prediction) in a CNN
在 GoogLeNet 中, 基本的卷积块称为 Inception 块
在 Inception 中由四条并行路径组成, 前三条路径使用窗口大小分别为 1x1, 3x3 和 5x5 的卷积层, 从不同的空间大小中提取信息. 中间两条路径在输入上执行 1x1 卷积, 以减少通道数, 从而降低模型的复杂性. 第四条路使用 3x3 最大池化层, 然后使用 1x1 的卷积层改变通道数. 这四条路都使用合适的填充来使得输入与输出的高和宽一致, 最后将每条线路的输出在通道维度上连结, 构成 Inception 块的输出. 超参数一般是每层的输出通道数

为什么 GoogLeNet 是有效的呢, 对于滤波器的各种组合, 可以使用不同的尺寸来探索图像, 意味着不同大小的滤波器可以有效地识别不同范围的图像细节,同时可以为不同的滤波器分配不同数量的参数

7-4-2 GoogLeNet 模型

GoogLeNet 一共使用了 9 个 Inception 块和全局平均池化层的堆叠来实现其估计值, Inception 块之间的最大池化层可以降低维度. 第一个模块类似于 AlexNet 和 LeNet, Inception 块的组合从 VGG 继承，全局平均汇聚层避免了在最后使用全连接层。

第一个模块
- 7x7 卷积：输出通道是 64，步幅是 2，填充是 3
- 3x3 最大池化：步幅是 2，填充是 1
第二个模块
- 1x1 卷积：输出通道 64
- 3x3 卷积：输出通道翻三倍 192，填充是 1
- 3x3 最大池化：步幅是 2，填充是 1
第三个模块
- Inception 模块
  - 输出通道数分别为 64 + 128 + 32 + 32 = 256，比例为 2：4：1：1
  - 第二个路径首先减少到一半（96/192 = 1/2)，第三个路径首先减少到 1/12 (16/192 = 1/12)
- Inception 模块
  - 输出通道数分别为 128 + 192 + 96 + 64 = 480，比例为 4：6：3：2
  - 第二个路径首先减少到一半（128/256 = 1/2)，第三个路径首先减少到 1/8 (32/256 = 1/12)
第四个模块
- Inception 模块
  - 输出通道数分别为 192 + 208 + 48 + 64 = 512，比例为 12：13：3：4
  - 第二个路径首先减少到 1/5 （96/480 = 1/5)，第三个路径首先减少到 1/12 (16/192 = 1/12)
- Inception 模块
  - 输出通道数分别为 160 + 224 + 64 + 64 = 512，比例为 5：7：2：2
  - 第二个路径首先减少到 7/32 （112/512 = 7/32)，第三个路径首先减少到 1/12 (3/64 = 1/12)
- Inception 模块
  - 输出通道数分别为 128 + 256 + 64 + 64 = 512，比例为 2：4：1：1
  - 第二个路径首先减少到 1/4 （128/512 = 1/4)，第三个路径首先减少到 1/64 (24/512 = 1/64)
- Inception 模块
  - 输出通道数分别为 112 + 288 + 64 + 64 = 528，比例为 7：18：4：4
  - 第二个路径首先减少到 9/32（144/512 = 9/32)，第三个路径首先减少到 1/16 (32/512 = 1/16)
- Inception 模块
  - 输出通道数分别为 256 + 320 + 128 + 128 = 832，比例为 4：5：2：2
  - 第二个路径首先减少到 10/33 （160/528 = 10/33)，第三个路径首先减少到 2/33 (32/528 = 2/33)
第五个模块
- Inception 模块
  - 输出通道数分别为 256 + 320 + 128 + 128 = 832，比例为 4：5：2：2
  - 第二个路径首先减少到 10/33 （160/832 = 10/33)，第三个路径首先减少到 2/33 (32/832 = 2/33)
- Inception 模块
  - 输出通道数分别为 384 + 384 + 128 + 128 = 1024，比例为 3：3：1：1
  - 第二个路径首先减少到 3/13 （192/832 = 3/13)，第三个路径首先减少到 3/56 (48/832 = 3/56)
全局池化层
- 将每个通道的高和宽改变为 1x1(类似于 NiN)
- 拉伸成二维
全连接层
- 输出的大小是预测的类别数

Inception 的变种

Inception-BN 使用了 batch normalization
Inception-V3 修改了 Inception 块
- 替换 5x5 为多个 3x3 卷积层
- 替换 5x5 为 1x7 和 7x1 卷积层
- 替换 3x3 为 1x3 和 3x1 卷积层
- 更深
- 段 3
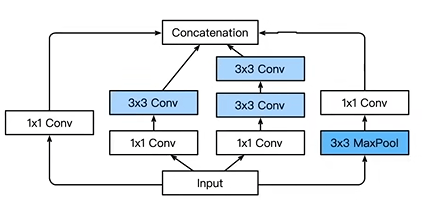
- 段 4
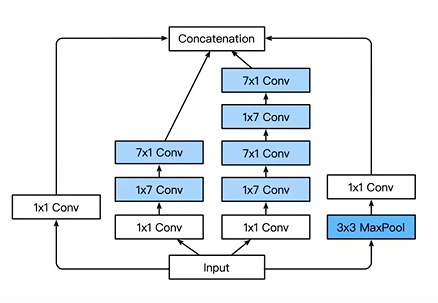
- 段 5
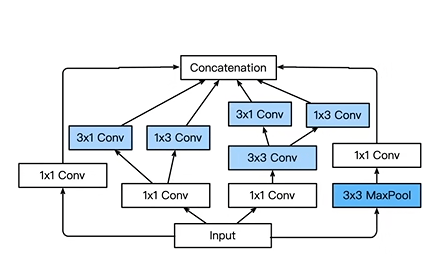
Inception-V4 使用残差连接

7-4-3 问答

1x1 可以降低复杂度，便于计算

怎么调参？

可以在 ImageNet 上的一个子集上调参

通道数越多，越可以匹配一些模式

训练 trick 对训练模型非常重要

使用 softmax label

7-5 批量归一化

批量归一化可以加速网络的收敛速度，同时结合残差块可以使得网络深度达到 100 层以上
本质：可能是通过在每个小批量里加入噪音来控制模型复杂度
结果：加速收敛速度，但一般不改变模型的精度

7-5-1 训练深层网络

为什么需要批量归一化呢？

数据预处理的方式对结果会产生很大的影响，在使用真实数据时，首先做的第一步是标准化输入特征，使其均值为 0，方差为 1，这种标准化可以很好的与优化器配合使用，能够将参数的量级进行统一
对于多层感知机或者卷积神经网络，中间层的变量可能会出现很大的变化范围：不论是沿着从输入到输出的层还是同一层中的单元，或者随着时间的推移，训练更新会出现意料不到的事情。批量归一化的提出者假设：这些变量分布的偏移可能会阻碍网络的收敛。直观的说，如果一个层的值的可变范围是另一个层的 100 倍，这时候，可能需要对学习率进行补偿调整
更深层的网络很复杂，容易过拟合，意味着正则化变得更加重要

批量归一化可应用于单个可选层（也可以应用到所有层），原理如下：每次额迭代训练中，首先规范化输入，即减去均值并除以其标准差，其中两者都基于当前小批量处理。接下来应用比例系数和比例偏移来恢复失去的自由度

在神经网络的不同层之间，将数据的不同层的分布固定住

对于批量为 1 的数据，应用 batch normalization 是没有意义的，因为减去均值以后就为 0 了，在应用 batch normalization 时，合适的 batch size 比是否采用 batch normalization 更重要，或者说，至少在我们可能调整批量大小时需要进行适当的校准。

从形式上来说， $x \in B$ 表示小批量 $B$ 的输入，批量规范化 BN 根据以下表达式转化 x：

BN (x) = γ ⊙ \frac{x - {\hat{μ}}_{B}}{{\hat{σ}}_{B}} + β .

${\hat{μ}}_{B}$ 表示小批量的均值， ${\hat{σ}}_{B}$ 表示小批量的标准差，应用 BN 后，生成的小批量的平均值为 0 和单位方差为 1，由于单位方差的选择是主观的，所以需要包含拉伸参数 scale $γ$ 和偏移参数 $β$ ，他们的形状和 x 相同且是需要学习的参数

通过以下方式计算 ${\hat{μ}}_{B}$ ， ${\hat{σ}}_{B}$

\begin{array}{r} \begin{aligned} {\hat{μ}}_{B} & = \frac{1}{| B |} \sum_{x \in B} x, \\ {\hat{σ}}_{B}^{2} & = \frac{1}{| B |} \sum_{x \in B} (x - {\hat{μ}}_{B})^{2} + ϵ . \end{aligned} \end{array}

在方差的估计值中，加入了一个小的常量 $ϵ$ ，以确保不会在 BN 中除以 0

在优化中，各种噪声源会导致更快的训练和较少的过拟合：这种变化似乎是正则化的一种形式，在一些研究中，分别将 BN 的性质和贝叶斯先验相关联

BN 在训练模式和预测模式中的功能不同，在训练过程中，我们无法得知整个数据集来估计平均值和方差，所以只能根据小批次的平均值和方差来不断训练模型，而在预测模式下，可以根据整个数据集精确计算批量规范化所需的平均值和方差

7-5-2 批量归一化层

对于全连接层和卷积层，批量规范化的实现方式略有不同

全连接层
将批量归一化置于全连接层中的仿射变换和激活函数之间，即

h = ϕ (BN (W x + b)) .

卷积层
在卷积层和非线性激活函数之前应用 BN，当卷积有多个输出通道时，需要对每个输出通道执行批量归一化，每个通道都有自己的拉伸参数 scale $γ$ 和偏移参数 $β$ ，假设小批量中包含 m 个样本，每个通道的输出高宽为 p q，对于卷积层在每个输出通道的 mpq 个元素上同时执行批量归一化

预测过程的批量归一化
对于在测试集上的数据，不需要对每个批次进行计算均值和方差，而是直接估算整个训练数据集的均值和方差，在预测过程中使用它们。可见，和暂退法(dropout)一样，批量规范化层在训练模式和预测模式下的计算结果也是不一样的。

7-5-3 问答

放在激活函数前：
ReLu 将输入转为正数，如果 BN 放在之后，有些输入又变回了负数。BN 属于线性变化
xavier 和 BN 有什么区别
-xavier 是在初始化阶段起作用，使得随机初始化的参数满足 normalization
BN 是在整个训练过程中起作用
马毅老师深度学习第一性原理论文作为白盒理论解释深度学习
assert len(x.shape) in (2, 4)
如果 len(x.shape)不是 2 或者 4，会报错，不会执行下面的内容
加了 BN 之后收敛时间缩短
每一批次的数据分布如果不相同的话，那么网络就要在每次迭代的时候都去适应不同的分布，这样会大大降低网络的训练速度
使用 BN 之后，可以使用更大的学习率，因此收敛时间会短一些
为什么可以使用更大的学习率
BN 可以缓解梯度消失问题，二是它对学习率不敏感
xxNormalization
大部分都是大同小异，处理的位置不一样

7-6 残差网络(ResNet)

7-6-1 函数类

首先假设有一类特定的神经网络架构 $F$ , 它包括学习速率和其他超参数设置，对于所有的 $f \in F$ ，存在一些参数集，这些参数可以通过在合适的数据集上进行训练而获得，假设 $f^{*}$ 是真正要找的函数，如果它是 $F$ 的子集，那么可以通过训练得到它。但如果不是，我们会尝试找到一个函数 $f_{F}^{*}$ ，这是在 $F$ 中最佳的选择，如可以按照如下优化方式得到

f_{F}^{*} := \underset{f}{argmin} L (X, y, f) subject to f \in F .

如何得到近似真正 $f^{*}$ 的函数呢，唯一合理的可能性是：需要设计一个更大，更强的架构 $F^{'}$ ，但是如果 $F ⊈ F^{'}$ 则无法保证新的体系更近似，事实上反而更糟。
对于下图，复杂度从 $F_{1}$ 到 $F_{6}$ 递增。在左图中，虽然 $F_{3}$ 比 $F_{1}$ 更接近，但 $F_{6}$ 离的更远了。而有图的嵌套函数则可以避免这个问题 (复杂度越大，越接近真正的f)

只有当复杂的函数类包含较小的函数类时，才能保证增加复杂度可以提高模型的性能。对于深度神经网络而言，如果可以将新添加的层训练成恒等映射（identity function） $f (x) = x$ ，则新模型和原模型同样有效，同时新模型还可能得到更优的解来拟合训练集。

7-6-2 残差块

假设输入的时 x，而希望学出的理想映射为 f(x)(作为激活激活函数的输出)，左图的虚线部分是直接拟合该映射 f(x)，而右图的虚线部分是拟合出残差映射 $f (x) - x$ ，残差映射往往更容易优化。如果希望学到的是恒等映射，只需将虚线部分的权重设置为 0 即可。当理想映射极其接近于恒等映射时，残差映射也很容易捕获到恒等映射的细微变化。
右图是 ResNet 的基础架构——残差块(residual blocks)，在残差块中，输入可以通过跨层数据线路更快的向前传播

ResNet 沿用了 VGG 完整的 3x3 卷积层设计。残差块里首先有 2 个相同输出通道的 3x3 卷积层，每个卷积层后面接一个批归一化层和 ReLU 激活函数，然后通过跨层数据通路，跳过这两个卷积运算，直接将输入加在最后 ReLU 激活函数之前。两个卷积的输入输出形状不变，如果需要改变通道数，需要额外引入 1x1 卷积层来将输入变换成需要的形状后再做相加运算
左侧是不包含 1x1 卷积的（通道数不变），右侧是包括的

7-6-3 ResNet 模型

ResNet 的前两层跟之前介绍的 GoogLeNet 中的一样：在输出通道数为 64，步幅为 2 的 7x7 卷积层之后接入步幅为 2 的 3x3 的最大池化层，不同之处在于 ResNet 每个卷积层之后加入了批归一化层
GoogLeNet 在后面接入了由四个 Inception 组成的模块，ResNet 则使用了由四个残差块组成的模块，每个模块使用若干个相同输出通道的残差块。第一个模块的通道数与输入通道数一致，由于使用了步幅为 2 的最大池化层，因此无须减少高宽。之后的每个模块第一个残差块将上一个的模块通道数翻倍，并将高宽减半
接着再 ResNet 中加入所有的残差块，每个模块使用 2 个残差块
最后加入全局平均池化层和全连接层

7-6-4 问答

当 batch_size 过大，收敛会有问题，因为整个 batch_size 里面有很多相似的图像，多样性不是那么好

问什么 f(x)=x + g(x)可以保证不会变坏
如果训练过程中，发现只用 x 就可以满足，那么反向传播的时候，g 就会拿不到梯度，不会更新，甚至权重最后变为 0

nn.ReLU(inplace = True)
可以原地处理，省内存

为什么 ResNet 能训练 1000 层以上
!http://cdn.zghhui.me/img/Pasted image 20231209093006.png

8 循环神经网络

8-1 序列模型

预测明天的股价要比过去的股价更加困难，在统计学中前者称为外推法，后者称为内插法。
音乐、语言、文本和视频都是连续的，如果顺序被重排，将会失去原有的意义
处理序列数据需要统计工具和新的神经网络架构

8-1-1 统计工具

用 $x_{t}$ 表示股价，即在时间步 $t \in Z^{+}$ 时观察的价格，t 一般是离散的，假设想预测 $x_{t}$ ，可以通过 $$ x_t \sim P(x_t \mid x_{t-1}, \ldots, x_1).$$
自回归模型
为了实现预测，可以通过回归模型实现，但输入数据的数量将会随着遇到的数据量的增加而增加，因此需要用近似的方法来处理

假设在实际情况下相当长的序列 $x_{t - 1}, \dots, x_{1}$ 是可能不必要的，因此只需要满足某个时间跨度 $τ$ 即可，即使用观测序列 $x_{t - 1}, \dots, x_{t - τ}$ ，这种方法的好处就在于参数的数量是不变的(t > $τ$ ), 这个模型就是自回归模型(autoregression models)
- 通过数据的前面的部分来做预测
保留一些对过去观测的总结 $h_{t}$ ,并且同时更新预测 ${\hat{x}}_{t}$ 和总结 $h_{t}$ , 这就产生了基于 ${\hat{x}}_{t} = P (x_{t} ∣ h_{t})$ 来估计 ${\hat{x}}_{t}$ ,以及公式 $h_{t} = g (h_{t - 1}, x_{t - 1})$ 更新的模型, 由于 $h_{t}$ ,没有被观测到,因此称为潜变量自回归模型(latent autoregression models)
如何生成训练数据?
一个经典的方法是使用历史观测来预测下一未来的观测,一个常见的假设是虽然特定值 $x_{t}$ 会变, 但是序列本身的动力学不会改变, 这样的假设是合理的, 因为新的动力学是受新的数据影响, 不可能用历史数据来预测新的动力学, 不变的动力学称为静止的(stationary)

P (x_{1}, \dots, x_{T}) = \prod_{t = 1}^{T} P (x_{t} ∣ x_{t - 1}, \dots, x_{1}) .

p (x) = p (x_{1}) \cdot p (x_{2} | x_{1}) \cdot p (x_{3} | x_{1}, x_{2}) \cdot \dots p (x_{T} | x_{1}, \dots x_{T - 1})

T 个变量的联合分布，其中各个变量之间是不独立的，可以用条件概率展开
如果处理的是离散的对象, 如单词, 上述考虑仍然有效, 唯一的差别是, 对于离散的对象, 需要使用分类器, 而不是回归模型来进行估计

马尔可夫模型
马尔可夫条件:
在自回归模型的近似法中, 使用 $x_{t - 1}, \dots, x_{t - τ}$ 来估计 $x_{t}$ （跟过去 $τ$ 个有关）, 只要这种是近似精确的, 就说序列满足马尔可夫条件(markov condition), 特别是如果 $τ = 1$ , 得到一个一阶马尔可夫模型(first-order markov model)

P (x_{1}, \dots, x_{T}) = \prod_{t = 1}^{T} P (x_{t} ∣ x_{t - 1}) 当 P (x_{1} ∣ x_{0}) = P (x_{1}) .

当假设 $x_{t}$ 是离散值时, 可以使用动态规划沿着马尔科夫链精确计算结果, 例如计算 $P (x_{t + 1} ∣ x_{t - 1})$

\begin{array}{r} \begin{aligned} P (x_{t + 1} ∣ x_{t - 1}) & = \frac{\sum_{x_{t}} P (x_{t + 1}, x_{t}, x_{t - 1})}{P (x_{t - 1})} \\ = \frac{\sum_{x_{t}} P (x_{t + 1} ∣ x_{t}, x_{t - 1}) P (x_{t}, x_{t - 1})}{P (x_{t - 1})} \\ = \sum_{x_{t}} P (x_{t + 1} ∣ x_{t}) P (x_{t} ∣ x_{t - 1}) \end{aligned} \end{array}

只需要考虑一个非常短的历史, $P (x_{t + 1} ∣ x_{t}, x_{t - 1}) = P (x_{t + 1} ∣ x_{t})$

因果关系
原则上, $P (x_{1}, \dots, x_{T})$ 倒序展开也没什么问题, 但将如果基于一个马尔可夫模型, 还可以得到一个反向的条件概率分布, 但是数据是存在着一个自然的方向, 即在时间上是前进的, 未来的事情没法改变过去, 即基于过去事件的分布是不会改变的.

8-2 文本预处理

对于序列数据处理问题，可以采用如下常见预处理步骤：

将文本作为字符串加载到内存中
将字符串拆分为词元
建立一个词表，将拆分的词元映射到数字索引
将文本转换为数字索引序列

8-2-1 读取数据

with open('time_machine', 'r') as f:
        lines = f.readlines()
    return [re.sub('[^A-Za-z]+', ' ', line).strip().lower() for line in lines]
    # strip是去掉首位的空格

8-2-2 词元化

将文本行列表（lines）作为输入，列表中的每个元素是一个文本序列（如一条文本行）。每个文本序列又被拆分成一个词元列表，词元（token）是文本的基本单位。最后，返回一个由词元列表组成的列表，其中的每个词元都是一个字符串（string）

8-2-3 词表

词元的类型是字符串，而模型需要的输入是数字，因此这种类型不方便模型使用。现在，让我们构建一个字典，通常也叫做词表（vocabulary），用来将字符串类型的词元映射到从 0 开始的数字索引中. 我们先将训练集中的所有文档合并在一起，对它们的唯一词元进行统计，得到的统计结果称之为语料 (corpus）然后根据每个唯一词元的出现频率，为其分配一个数字索引。很少出现的词元通常被移除，这可以降低复杂性
语料库中不存在或已删除的任何词元都将映射到一个特定的未知词元 <unk>。我们可以选择增加一个列表，用于保存那些被保留的词元，
例如：填充词元（ <pad> ）；序列开始词元（ <bos> ）；序列结束词元（ <eos> ）。

8-3 语言模型

假设长度为 T 的文本序列的词元依次为 $x_{1}, x_{2}, \dots, x_{T}$ ，于是 $x_{t}$ 可以被认为是文本序列在时间步 t 处的观测或标签，给定这样的文本序列时，语言模型的目标是估计序列的联合概率 $P (x_{1}, x_{2}, \dots, x_{T}) .$

8-3-1 学习语言模型

依靠对序列模型的分析，从基本概率规则开始：

P (x_{1}, x_{2}, \dots, x_{T}) = \prod_{t = 1}^{T} P (x_{t} ∣ x_{1}, \dots, x_{t - 1}) .

为了训练语言模型，需要计算单词的概率，以及给定前面几个单词后出现某个单词的条件概率，这些概率本质上是语言模型的参数

p (x, x^{'}, x^{″}) = p (x) p (x^{'} | x) p (x^{″} | x, x^{'}) = \frac{n (x)}{n} \frac{n (x, x^{'})}{n (x)} \frac{n (x, x^{'}, x^{″})}{n (x, x^{'})}

在预测时，随着词组越长，虽然可能是存在的，但在数据集中却很少或者找不到，这些将导致在语言模型中无法进行正确预测。

一种常见的策略是拉普拉斯平滑，具体的方法是在计数中添加一个小常量，用 n 表示训练集中的单词总数，m 表示唯一单词的数量，此解决办法有助于处理单元素的问题

\begin{array}{r} \begin{aligned} \hat{P} (x) & = \frac{n (x) + ϵ_{1} / m}{n + ϵ_{1}}, \\ \hat{P} (x^{'} ∣ x) & = \frac{n (x, x^{'}) + ϵ_{2} \hat{P} (x^{'})}{n (x) + ϵ_{2}}, \\ \hat{P} (x^{″} ∣ x, x^{'}) & = \frac{n (x, x^{'}, x^{″}) + ϵ_{3} \hat{P} (x^{″})}{n (x, x^{'}) + ϵ_{3}} . \end{aligned} \end{array}

其中ε是超参数，当为 0 时不应用平滑，当接近无穷大时，P(x)的概率接近均匀分布 1/m，但是这样的模型很容易变得无效，首先是要存储所有的计数，其次是完全忽略了单词的意思，三是长单词序列大部分没有出现过

8-3-2 马尔可夫模型和 n 元语法

一阶马尔可夫性质： $P (x_{t + 1} ∣ x_{t}, \dots, x_{1}) = P (x_{t + 1} ∣ x_{t})$ ，阶数越高，对应的依赖关系越长。这种性质推导出了很多应用于建模的近似公式

\begin{array}{r} \begin{aligned} P (x_{1}, x_{2}, x_{3}, x_{4}) & = P (x_{1}) P (x_{2}) P (x_{3}) P (x_{4}), \\ P (x_{1}, x_{2}, x_{3}, x_{4}) & = P (x_{1}) P (x_{2} ∣ x_{1}) P (x_{3} ∣ x_{2}) P (x_{4} ∣ x_{3}), \\ P (x_{1}, x_{2}, x_{3}, x_{4}) & = P (x_{1}) P (x_{2} ∣ x_{1}) P (x_{3} ∣ x_{1}, x_{2}) P (x_{4} ∣ x_{2}, x_{3}) . \end{aligned} \end{array}

通常，涉及一个，两个和三个变量的概率公式分别被称为一元语法、二元语法和三元语法模型

8-3-3 自然语言统计

使用语言预处理可以得到词表，一般出现次数最多的词是停用词，可以被过滤掉，此外词频的衰减速度很快，除了停用词以外，剩余的单词满足双对数坐标图上的一条直线，即满足齐普夫定律，即第 i 个最常用的单词的频率为 $n_{i}$

\log n_{i} = - α \log i + c,

其中 a 是刻画分布的指数，c 是常数，这表明通过计数和平滑建模单词是不可行的，这样建模的结果往往会高估尾部单词的频率

结果：

除了一元语法词，单词序列似乎遵守齐普夫定律
词表中 n 元组的数量没有那么大，表面语言中存在相当多的结构
N 元组很少出现，使得拉普拉斯平滑不适合语言建模，可以使用深度学习模型

8-3-4 读取长序列数据

序列数据本质上是连续的，因此在处理数据时需要解决这个问题，当序列变得太长而不能被模型一次性全部处理时，我们可能希望拆分这样的序列方便模型读取。
总体策略：
假设我们将使用神经网络来训练语言模型，模型中的网络一次处理具有预定义长度（例如 n 个时间步）的一个小批量序列。现在的问题是如何随机生成一个小批量数据的特征和标签以供读取。
由于文本序列可以是任意长的，于是任意长的序列可以被我们划分为具有相同时间步数的子序列。当训练我们的神经网络时，这样的小批量子序列将被输入到模型中。假设网络一次只处理具有 n 个时间步的子序列，其中每个时间步的词元对应于一个字符，可以选择任意偏移量来指示初始位置。

如何进行选择？
如果我们只选择一个偏移量，那么用于训练网络的、所有可能的子序列的覆盖范围将是有限的。因此，我们可以从随机偏移量开始划分序列，以同时获得 覆盖性（coverage）和 随机性（randomness）

随机采样
在随机采用中，每个样本都是在原始的长序列上任意捕获的子序列，在迭代过程中，来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻，对于语言模型，目标是基于到目前位置看到的词元来预测下一个词元，因此标签时移位了一个词元的原始序列

顺序分区
除了随机抽样，还可以保证两个相邻的小批量中的子序列在原始顺序上也是相邻的，这种策略在基于小批量的迭代过程中保留了拆分的子序列的顺序，因此称为顺序分区。

8-4 循环神经网络

对于 n 元语法模型，其中单词 $x_{t}$ 在时间步 t 的条件概率取决于前面 n-1 个单词，如果要使用时间步 t-（n-1）之前的单词，需要增加 n，这样会导致 n 会变得非常大（指数增长）因此不如使用隐变量模型：

P (x_{t} ∣ x_{t - 1}, \dots, x_{1}) \approx P (x_{t} ∣ h_{t - 1}),

隐藏层和隐状态时两个不同的概念，隐藏层是从输入到输出的路径上的隐藏的层，隐状态是在给定步骤所做的任何事情的输入，并且这些状态只能通过先前时间步的数据来计算

8-4-1 有隐状态的循环神经网络

在无隐状态时，隐藏层的输出通过下式计算：

H = ϕ (X W_{x h} + b_{h}) .

在引入隐状态之后，还需要保存前一步的隐变量 $H_{t - 1}$ , 并引入一个新的权重参数 $W_{h h}$ , 并通过以下公式计算输出

H_{t} = ϕ (X_{t} W_{x h} + H_{t - 1} W_{h h} + b_{h}) .

从相邻时间步的隐变量 $H_{t}$ 和 $H_{t - 1}$ 之间的关系可知，这些变量的获取保留了序列直到其当前时间步的历史信息，就如当前时间步下神经网络的状态或者记忆，因此这样的隐变量定义为隐状态。由于当前时间步中，隐状态使用的定义和前一个时间步使用的定义相同，因此计算是循环的，基于循环计算的隐状态神经网络被命名为循环神经网络（recurrent nn），在循环神经网络执行计算的层称为循环层
循环神经网络的参数包括 $W_{x h} \in R^{d \times h}, W_{h h} \in R^{h \times h}$ 和偏置 $b_{h} \in R^{1 \times h}$ 以及输出层的权重 $W_{h q} \in R^{h \times q}$ ，在不同的时间步，循环神经网络也总是使用这些参数，因此开销不会随着时间步的增加而增加

循环神经网络的计算逻辑：

拼接当前的时间步 $X_{t - 1}$ 和前一步的隐状态 $H_{t - 1}$
将拼接结果送入带有激活函数的全连接层,输出是当前时间步 t 的隐状态 $H_{t}$

隐状态的 $X_{t} W_{x h} + H_{t - 1} W_{h h}$ 计算相当于 X 和 H 的拼接和 W 和 W 的拼接的矩阵乘法

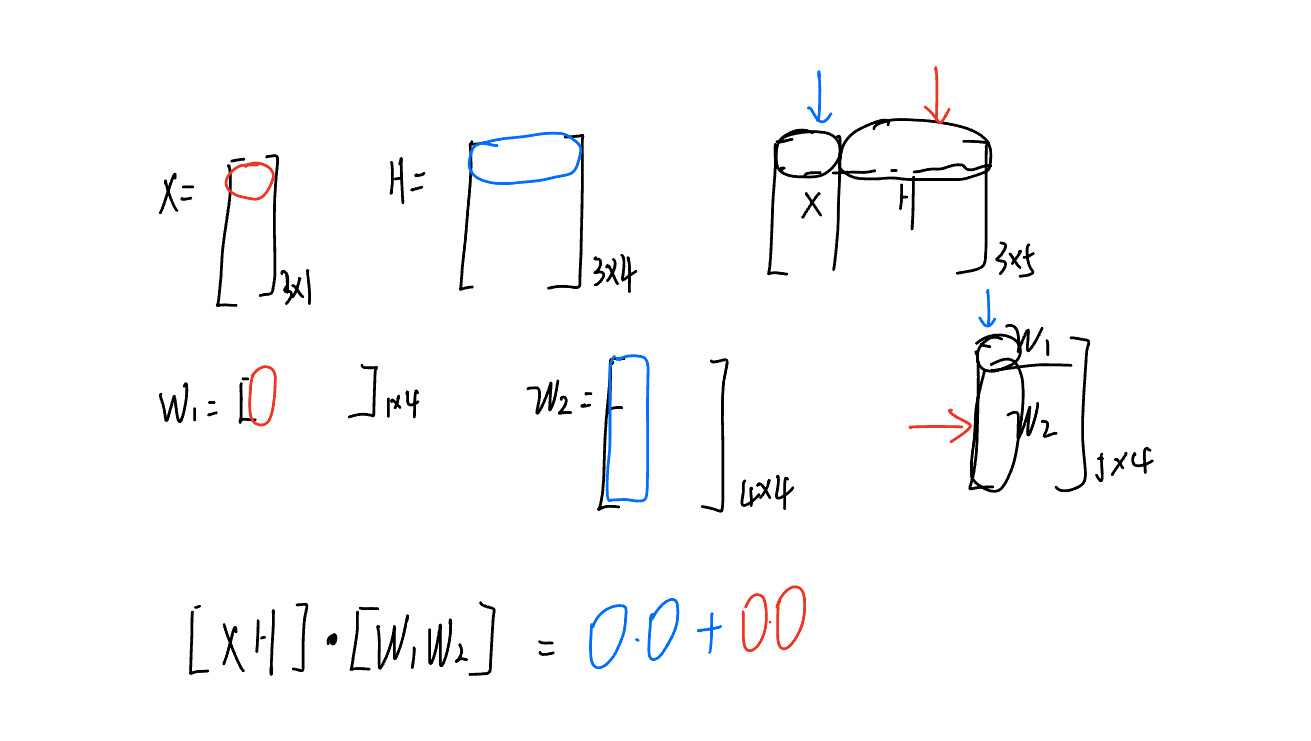
8-4-3 基于循环神经网络的字符级语言模型

当考虑用字符级语言模型时,使用当前的和先前的字符预测下一个字符,以 machin 为例

在训练过程中, 对每个时间步的输出进行 softmax 操作, 利用交叉熵损失函数计算输出和标签的损失, 比如第三步的损失是由文本序列 m a c 决定的下一个字符的分布与标签 h 的损失

8-4-4 困惑度 Perplexity

如何衡量语言模型的质量? 一个好的语言模型能够用高度准确的词元来预测接下来是什么,可以通过序列的似然概率来度量模型的质量, 但是较短的序列会比较长的序列更有可能出现, 因此这一方法不太好.

可以使用信息熵来衡量, 具体是指, 当词元集去预测下一个词元的时候, 更好的模型应当更能准确的预测下一个词元, 因此可以使用一个序列中所有词元的交叉熵损失的平均值来衡量

\frac{1}{n} \sum_{t = 1}^{n} - \log P (x_{t} ∣ x_{t - 1}, \dots, x_{1}),

实际上, 更喜欢采用困惑度 perplexity 来衡量, 他是上式的指数

\exp (- \frac{1}{n} \sum_{t = 1}^{n} \log P (x_{t} ∣ x_{t - 1}, \dots, x_{1})) .

最好的情况是 1, 最坏的情况是∞ 平均情况是: 模型的预测是所有词元的均匀分布, 困惑度等于表中为唯一词元的数量 $p = l o g (\frac{1}{m})$

梯度裁剪
当计算 T 时间步长上的梯度时，在反向传播的过程中，会产生 O(T) 的矩阵乘法链，导致数值不稳定，使用梯度裁剪可以预防梯度爆炸

如果梯度长度小于θ，则拖影回长度θ
$g ⬅ m i n (1, \frac{θ}{∣∣ g ∣∣}) g$ ，其中 g 表示所有梯度组成的向量
更多 RNNs

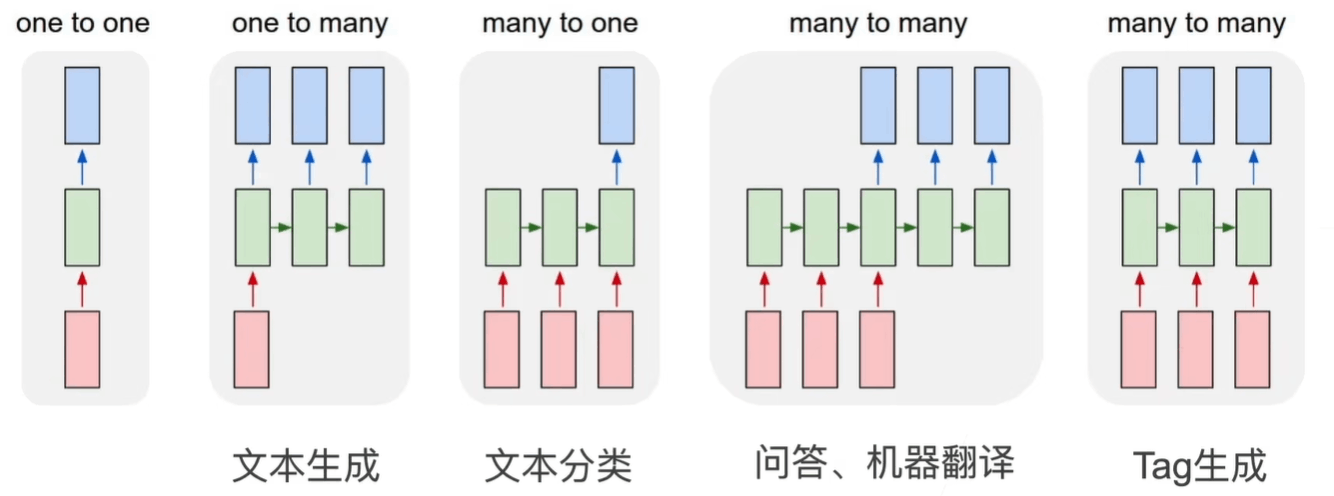
RNN 求解梯度的细节
!http://cdn.zghhui.me/img/Pasted image 20231217150441.png

!http://cdn.zghhui.me/img/Pasted image 20231217150518.png

9 现代循环神经网络

循环神经网络可以处理序列数据，但它常见的一个问题是数值不稳定，虽然梯度裁剪可以缓解这个问题，但仍需要设计更加复杂的模型来处理它，即门控循环单元和长短期记忆网络，然后基于一个单向隐藏层来扩展循环神经网络的架构

9-1 门控循环单元 GRU

梯度异常的一些实际情况：

早期的观测值对于未来的观测值非常有意义，如第一个观测值包含一个校验和，目标是在序列的末尾辨别校验和是否正确
序列中一些词元没有相关的观测值，希望可以跳过这些词元
序列的各个部分之间会存在着逻辑中断，希望可以重置内部状态表示

门控循环单元是长短期记忆网络的一个变体，一般有着相似的效果，但速度明显更快

9-1-1 门控隐状态

门控循环单元与普通循环神经网络之间的关键区别在于：前者支持隐状态的门控，意味着模型有专门的机制来确定何时更新隐状态，以及何时重置状态，这些机制是可学习的，并能够解决上面的问题。

重置门(reset gate) 和更新门(update gate)
一般设置成(0, 1)之间的向量, 这一可以进行凸优化组合。重置门允许控制"可能还想记住的"过去的状态的数量；更新门将允许控制新状态中有多少个是旧状态的副本

两个门的输入是上一个隐状态和当前时间步的输入，输出是使用 sigmoid 激活函数的两个全连接层，计算：

\begin{array}{r} \begin{matrix} R_{t} = σ (X_{t} W_{x r} + H_{t - 1} W_{h r} + b_{r}), \\ Z_{t} = σ (X_{t} W_{x z} + H_{t - 1} W_{h z} + b_{z}), \end{matrix} \end{array}

候选隐状态
将重置门(R)和常规隐状态更新机制集成，得到在时间步 t 的候选隐状态 $\hat{H_{t } } $

{\tilde{H}}_{t} = \tanh (X_{t} W_{x h} + (R_{t} ⊙ H_{t - 1}) W_{h h} + b_{h}),

符号 $⊙$ 表示按元素乘积，使用 tanh 非线性激活函数使得候选隐状态中的值保持在(-1, 1)中
使用 R 和 H 的元素相乘可以减少以往状态的影响，每当重置门 R 中的项接近于 1 时，恢复成一个普通的循环神经网络，当接近于 0 时，候选隐状态是以 Xt 作为输入的多层感知机的结果，因此任何预先存在的隐状态都会被重置为默认值

隐状态
隐状态的计算需要结合更新门的效果，这一步确定新的隐状态在多大程度上来自旧状态 $H_{t - 1}$ 和新的候选状态 ${\tilde{H}}_{t}$ 。更新门 Zt 仅需要在 $H_{t - 1}$ 和 ${\tilde{H}}_{t}$ 之间按元素进行凸组合就可以实现这个目标，这就得出了门控循环单元的最终更新公式：

H_{t} = Z_{t} ⊙ H_{t - 1} + (1 - Z_{t}) ⊙ {\tilde{H}}_{t} .

每当 Zt 接近于 1 时，模型就倾向于保存旧状态，此时 Xt 得信息就会被忽略，从而可以跳过依赖链条中得时间步 t，相反，Zt 接近于 0 时，新的隐状态就会接近于候选隐状态。这些设计可以更好的处理梯度消失的问题，并捕捉时间步距离很长的依赖关系。如果整个子序列的所有时间步的更新门都接近于1，则无论序列的长度如何，在序列起始时间步的旧隐状态都将很容易保留并传递到序列结束。

9-2 长短期记忆网络 LSTM

隐变量模型存在着长期信息保存和短期输入缺失的问题，解决这一问题的最早方法是长短期存储器 LSTM，跟 GRU 差不多，但要更复杂一些

9-2-1 门控记忆元

长短期记忆网络引入了记忆元(memory cell)或者简称单元(cell)，它与隐状态有着相同的形状，设计的目的在于记录附加的信息。为了控制记忆元，需要用到很多的门，其中一个门是用来从单元中输出条目，称为输出门(output gate)，另外一个门是用来决定什么时候将输入读入单元，称为输入门(input gate)；还需要一种机制来重置单元的内容，称为遗忘门(forget gate)

当前时间步的输入和前一个时间步的隐状态作为数据送入到长短期记忆网络的门中，它们由三个具有 sigmoid 激活函数的全连接层处理，以计算输入门、输出门、遗忘门的值，三个门的值在(0, 1)之间

\begin{array}{r} \begin{aligned} I_{t} & = σ (X_{t} W_{x i} + H_{t - 1} W_{h i} + b_{i}), \\ F_{t} & = σ (X_{t} W_{x f} + H_{t - 1} W_{h f} + b_{f}), \\ O_{t} & = σ (X_{t} W_{x o} + H_{t - 1} W_{h o} + b_{o}), \end{aligned} \end{array}

候选记忆元
候选记忆元的计算方式和三个门的方法相同，但使用 tanh 作为激活函数，值在(-1, 1)之间

{\tilde{C}}_{t} = tanh (X_{t} W_{x c} + H_{t - 1} W_{h c} + b_{c}),

记忆元
在 LSTM 中，输入门 It 来控制采用多少来自候选记忆元 $\hat{C_{t } } $ 而遗忘门 Ft 则控制保留多少过去的记忆元 $C_{t - 1}$ 的内容，按元素乘法

C_{t} = F_{t} ⊙ C_{t - 1} + I_{t} ⊙ {\tilde{C}}_{t} .

如果遗忘门始终为 1，而输入门始终为 0，则过去的记忆元则被传递到当前的时间步，引入这种设计是为了缓解梯度消失问题，并更好地捕获序列中的长距离依赖关系。

隐状态
隐状态 Ht 的计算依靠输出门 O，在 LSTM 中，仅仅是记忆元的 tanh 的门控版本，确保了 Ht 的值在区间(-1, 1)之间
只要输出门接近1，我们就能够有效地将所有记忆信息传递给预测部分，而对于输出门接近0，我们只保留记忆元内的所有信息，H 被重置

H_{t} = O_{t} ⊙ \tanh (C_{t}) .

9-3 深度循环神经网络

可以将多层循环神经网络堆叠在一起，通过几个简单层的组合，产生一个灵活的机制，特别是，数据可能和不同层的堆叠有关。

假设在时间步 t 有一个小批量的输入数据 $X_{t} \in R^{n \times d}$ （样本数是 n，每个样本的输入数是 d），同时将第 l 层隐藏层的隐状态设为 $H_{t}^{(l)} \in R^{n \times h}$ （隐单元数 h）输出层变量设为 $O_{t} \in R^{n \times q}$ （输出数 q）设置 $H_{t}^{(0)} = X_{t}$ ，第 l 个隐藏层状态使用激活函数 $ϕ_{l}$

H_{t}^{(l)} = ϕ_{l} (H_{t}^{(l - 1)} W_{x h}^{(l)} + H_{t - 1}^{(l)} W_{h h}^{(l)} + b_{h}^{(l)}),

输出层的计算仅基于 L 层的隐状态

O_{t} = H_{t}^{(L)} W_{h q} + b_{q},

与多层感知机类似，隐藏层数目 L 和隐单元数目 h 都是超参数，用 GRU 或者 LSTM 作为隐状态计算，可以得到深层门控循环神经网络和深度长短期记忆神经网络

9-4 双向循环神经网络

9-4-1 隐马尔可夫模型的动态规划

设计一个隐变量模型：在任意时间步 t，假设存在一个隐变量 $h_{t}$ ，通过概率 $P (x_{t} ∣ h_{t})$ 控制观测到的 Xt，此外任何一个 $h_{t} \to h_{t + 1}$ 都是一些状态转移概率 $P (h_{t + 1} ∣ h_{t})$ 给出的，这个概率图模型就是隐马尔可夫模型

对于有 T 个观测值的序列，在观测状态和隐状态上具有以下联合概率分布：

P (x_{1}, \dots, x_{T}, h_{1}, \dots, h_{T}) = \prod_{t = 1}^{T} P (h_{t} ∣ h_{t - 1}) P (x_{t} ∣ h_{t}), where P (h_{1} ∣ h_{0}) = P (h_{1}) .

9-4-2 双向循环神经网络

对于在时间步 t 有一个小批量的输入数据 $X_{t} \in R^{n \times d}$ （样本数是 n，每个样本的输入数是 d），隐藏层状态使用激活函数 $ϕ_{l}$ 。在双向架构中，前向状态和反向状态分别为 ${\vec{H}}_{t} \in R^{n \times h}$ 和 ${\overset{\leftarrow}{H}}_{t} \in R^{n \times h}$ ，其中 h 是隐藏单元的数目

\begin{array}{r} \begin{aligned} {\vec{H}}_{t} & = ϕ (X_{t} W_{x h}^{(f)} + {\vec{H}}_{t - 1} W_{h h}^{(f)} + b_{h}^{(f)}), \\ {\overset{\leftarrow}{H}}_{t} & = ϕ (X_{t} W_{x h}^{(b)} + {\overset{\leftarrow}{H}}_{t + 1} W_{h h}^{(b)} + b_{h}^{(b)}), \end{aligned} \end{array}

共有六个参数
然后将前向隐状态 ${\vec{H}}_{t}$ 和反向隐状态 ${\overset{\leftarrow}{H}}_{t}$ 连接起来，获取需要送入输出层的隐状态 $H_{t} \in R^{n \times 2 h}$ ，在具有多个隐藏层的深度双向循环神经网络中，该信息作为输入传递到下一个双向层。最后，输出层计算得到的输出为 $O_{t} \in R^{n \times q}$

O_{t} = H_{t} W_{h q} + b_{q} .

9-4-3 计算代价

双向循环神经网络的一个关键特性是：使用来自序列两端的信息来估计输出。因此需要知道过去和未来的内容来预测现在。因此对于单向预测而言，效果很差。
双向循环神经网络的计算非常慢，其主要原因是网络的前向传播需要在双向层中进行前向和后向递归，并且网络的反向传播还依赖于前向传播的结果。因此，梯度求解将有一个非常长的链。
双向层的使用在实践中非常少，并且仅仅应用于部分场合。例如，填充缺失的单词、词元注释

10 注意力机制

10-1 注意力提示

10-1-1 生物学中的注意力提示

可以分为自主性和非自主性提示

非自主性提示是基于物体的突出性和易见性
自主性是受到了认知和意识的控制

10-1-2 查询、键和值

是否包含自主性提示将注意力机制和全连接层或者汇聚层区分开来，在注意力机制的背景下，自主性提示称为查询（query）给定任何查询，注意力机制通过注意力池化（attention pooling）将选择引导至感官输入（sensory inputs，如中间特征表示）在注意力机制中，这些感官输入称为值（value）更为通俗的表示是每个值都与一个键（key）配对，可以想象为感官输入的非自主性提示。可以通过设计注意力池化的方式，便于给定的查询（自主性提示）与键（非自主性提示）进行匹配，这将引导得出最匹配的值（感官输入）。

10-1-3 注意力的可视化

平均汇聚层可以视为输入的加权平均值，其各输入的权重是一样的。实际上，注意力池化得到的是加权平均的总和值，其中权重是在给定的查询和不同的键之间计算得出的。

10-2 注意力池化：Nadaraya-Watson 核回归

通过学习 $f$ 来预测任意新输入 $x$ 的输出 $\hat{y} = f (x)$

10-2-1 平均汇聚

f (x) = \frac{1}{n} \sum_{i = 1}^{n} y_{i}

10-2-2 非参数注意力池化

在平均汇聚中，忽略了 $x_{i}$ ，于是 N 和 W 提出了根据输入的位置对输出 $y_{i}$ 进行加权：

f (x) = \sum_{i = 1}^{n} \frac{K (x - x_{i})}{\sum_{j = 1}^{n} K (x - x_{j})} y_{i},

其中 K 是核，公式所描述的估计器被称为 Nadaraya-Watson 核回归，受此启发可以从注意力机制框架重写公式，称为一个更加通用的注意力池化（attention pooling）公式

f (x) = \sum_{i = 1}^{n} α (x, x_{i}) y_{i},

其中 $x$ 是查询, $(x_{i}, y_{i})$ 是键值对,比较上式和上上式,注意力池化是 $y_{i}$ 的加权平均. 将查询 $x$ 和键 $x_{i}$ 之间的关系建模为注意力权重 $α (x, x_{i})$ ,这个权重分配给每一个对应值 $y_{i}$ , 对于任何查询, 模型所有键值对注意力权重都是一个有效的概率分布: 它们是非负的, 且总和为 1
考虑一个高斯核,其定义为:

K (u) = \frac{1}{\sqrt{2 π}} \exp (- \frac{u^{2}}{2}) .

将高斯核带入可以得到:

\begin{array}{r} \begin{aligned} f (x) & = \sum_{i = 1}^{n} α (x, x_{i}) y_{i} \\ = \sum_{i = 1}^{n} \frac{\exp (- \frac{1}{2} (x - x_{i})^{2})}{\sum_{j = 1}^{n} \exp (- \frac{1}{2} (x - x_{j})^{2})} y_{i} \\ = \sum_{i = 1}^{n} softmax (- \frac{1}{2} (x - x_{i})^{2}) y_{i} . \end{aligned} \end{array}

如果一个键 $x_{i}$ 更加接近于给定的查询 $x$ , 那么分配给这个键对应值 $y_{i}$ 的注意力权重也就越大
Nadaraya-Watson 核回归是一个非参数模型, 即非参数的注意力池化模型

10-2-3 带参数注意力池化

非参数的 Nadaraya-Watson 核回归具有 一致性（consistency）的优点：如果有足够的数据，此模型会收敛到最优结果。尽管如此，我们还是可以轻松地将可学习的参数集成到注意力池化中。
与非参数注意力池化不同, 多了一个可学习得 $w$

\begin{array}{r} \begin{aligned} f (x) & = \sum_{i = 1}^{n} α (x, x_{i}) y_{i} \\ = \sum_{i = 1}^{n} \frac{\exp (- \frac{1}{2} ((x - x_{i}) w)^{2})}{\sum_{j = 1}^{n} \exp (- \frac{1}{2} ((x - x_{j}) w)^{2})} y_{i} \\ = \sum_{i = 1}^{n} softmax (- \frac{1}{2} ((x - x_{i}) w)^{2}) y_{i} . \end{aligned} \end{array}

10-3 注意力评分函数

10-2 节使用了高斯核来对查询和键之间的关系尽心建模. 高斯核指数部分可以视为注意力评分函数(attention scoring function)简称评分函数, 然后把这个函数的输出结果输入到 softmax 中运算, 通过上述步骤得到与键相对应的值的概率分布(注意力权重), 最后注意力的汇聚输出就是基于这些注意力权重的值的加权和
上述算法可以用来实现下图的注意力机制框架, $α$ 表示评分函数

用数学语言描述, 假设有一个查询 $q \in R^{q}$ 和 m 个键值对 $(k_{1}, v_{1}), \dots, (k_{m}, v_{m})$ , 其中 $k_{i} \in R^{k}$ , 注意力池化函数 $f$ 就被表示为值得加权和:

f (q, (k_{1}, v_{1}), \dots, (k_{m}, v_{m})) = \sum_{i = 1}^{m} α (q, k_{i}) v_{i} \in R^{v},

其中查询 q 和键 k 的注意力权重是通过注意力评分函数α将两个向量映射成标量, 在经过 softmax 运算得到的:

α (q, k_{i}) = softmax (a (q, k_{i})) = \frac{\exp (a (q, k_{i}))}{\sum_{j = 1}^{m} \exp (a (q, k_{j}))} \in R .

10-3-1 掩蔽 softmax 操作

softmax 操作用于输出一个概率分布作为注意力权重。在某些情况下，并非所有的值都应该被纳入到注意力池化中。例如，为了在 9.5节中高效处理小批量数据集，某些文本序列被填充了没有意义的特殊词元。为了仅将有意义的词元作为值来获取注意力池化，可以指定一个有效序列长度（即词元的个数），以便在计算 softmax 时过滤掉超出指定范围的位置。下面的 masked_softmax 函数实现了这样的_掩蔽 softmax 操作_（masked softmax operation），其中任何超出有效长度的位置都被掩蔽并置为0。

10-3-2 加性注意力

当查询和键是不同长度的矢量时, 可以使用加性注意力作为评分函数. 给定查询 q 和键 k, 加性注意力(additive attention)的评分函数是:

a (q, k) = w_{v}^{⊤} tanh (W_{q} q + W_{k} k) \in R,

三个 w 都是可学习的参数
将查询和键连结起来后输入到一个多层感知机（MLP）中，感知机包含一个隐藏层，其隐藏单元数是一个超参数ℎ。通过使用 tanh 作为激活函数，并且禁用偏置项

10-3-3 缩放点积注意力
使用点积可以得到计算效率更高的评分函数，但是点积操作要求查询和键具有相同的长度 d。假设查询和键的所有元素都是独立的随机变量，并且都满足零均值和单位方差，那么两个向量的点积的均值为0，方差为 d。为确保无论向量长度如何，点积的方差在不考虑向量长度的情况下仍然是1，我们再将点积除以 $\sqrt{d}$ ，则 缩放点积注意力

a (q, k) = q^{⊤} k / \sqrt{d} .

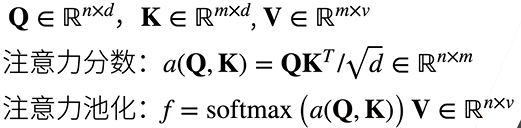
10-4 Bahdanau 注意力

10-5 多头注意力

在实践中，当给定相同的查询、键和值的集合时，我们希望模型可以基于相同的注意力机制学习到不同的行为，然后将不同的行为作为知识组合起来，捕获序列内各种范围的依赖关系（例如，短距离依赖和长距离依赖关系）。因此，允许注意力机制组合使用查询、键和值的不同 子空间表示（representation subspaces）可能是有益的。
为此，与其只使用单独一个注意力池化，我们可以用独立学习得到的ℎ组不同的 线性投影（linear projections）来变换查询、键和值。然后，这ℎ组变换后的查询、键和值将并行地送到注意力池化中。最后，将这ℎ个注意力池化的输出拼接在一起，并且通过另一个可以学习的线性投影进行变换，以产生最终输出。这种设计被称为 多头注意力（multihead attention）。对于ℎ个注意力池化输出，每一个注意力池化都被称作一个头（head）。图10.5.1 展示了使用全连接层来实现可学习的线性变换的多头注意力。

10-5-1 模型

在实现多头注意力之前, 我们先用数学语言来将这个模型形式化描述出来. 给定查询, 给定查询 q, 键 k 和值 v, 每个注意力头 $h_{i} (i = 1 \dots h)$ 的计算方法为:

h_{i} = f (W_{i}^{(q)} q, W_{i}^{(k)} k, W_{i}^{(v)} v) \in R^{p_{v}},

可学习的参数包括三个 W 以及代表注意力池化的函数 f, f 可以是加性注意力和缩放点积注意力. 多头注意力的输出需要经过另外一个线性转换, 它对应着 h 个头连结后的结果,因此其可学习的参数是 $W_{o}$

\begin{array}{r} W_{o} [\begin{array}{c} h_{1} \\ ⋮ \\ h_{h} \end{array}] \in R^{p_{o}} . \end{array}

10-6 自注意力和位置编码

有了注意力机制之后，我们将词元序列输入注意力池化中，以便同一组词元同时充当查询、键和值。具体来说，每个查询都会关注所有的键－值对并生成一个注意力输出。由于查询、键和值来自同一组输入，因此被称为 自注意力（self-attention）

10-6-1 自注意力

给定一个由词元组成的输入序列 $x_{1}, \dots, x_{n}$ , 该序列的自注意力输出为一个长度相同的序列 $y_{1}, \dots, y_{n}$ , 其中:

y_{i} = f (x_{i}, (x_{1}, x_{1}), \dots, (x_{n}, x_{n})) \in R^{d}

10-6-2 比较卷积神经网络、循环神经网络和自注意力

具体来说，将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意，顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能更轻松地学习序列中的远距离依赖关系

考虑一个卷积核大小为 k 的卷积层, 由于序列长度是 n,输入和输出通道都是 d, 所以卷积层的计算复杂度是 $O (k n d^{2})$ , 最大路径长度是 $O (n / k)$ , 有 $O (1)$ 个顺序操作
当更新循环神经网络的隐状态时, d x d 权重矩阵和 d 维隐状态的乘法计算复杂度为 $O (d^{2})$ , 由于序列长度为 n, 因此循环神经网络层的计算复杂度为 $O (n d^{2})$ , 有 n 个顺序操作无法并行优化, 最大路径长度也是 O(n)
在自注意力中，查询、键和值都是 n×d 矩阵。考虑 (10.3.5) 中缩放的”点－积“注意力，其中 n×d 矩阵乘以 dxn 矩阵。之后输出的 nxn 矩阵乘以 nxd 矩阵。因此，自注意力具有 $O (n^{2} d)$ 计算复杂性。正如在图10.6.1 中所讲，每个词元都通过自注意力直接连接到任何其他词元。因此，有 O(1)个顺序操作可以并行计算，最大路径长度也是 O(1)。

10-6-3 位置编码

为了在注意力机制中使用顺序信息，通过在输入表示中添加位置编码（positional encoding）来注入绝对或者相对的位置信息。位置信息可以通过学习也可以通过直接固定得到，具体实现上来讲是通过基于正弦函数或者余弦函数的规定位置编码
假设输入表示 $X$ 包含一个序列中的 n 个词元的 d 维嵌入表示，位置编码使用相同形状的位置嵌入矩阵 P，输出 X+P，矩阵第 i 行第 2j 和 2j+1 列上的元素为：

\begin{array}{r} \begin{aligned} p_{i, 2 j} & = \sin (\frac{i}{10000^{2 j / d}}), \\ p_{i, 2 j + 1} & = \cos (\frac{i}{10000^{2 j / d}}) . \end{aligned} \end{array}

绝对位置信息
在二进制表示中，较高比特位的交替频率低于较低比特位，与下面的热图所示相似，只是位置编码通过使用三角函数在编码维度上降低频率。由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间。
相对位置信息
除了捕获绝对位置信息之外，上述的位置编码还允许模型学习得到输入序列中相对位置信息。这是因为对于任何确定的位置偏移δ，位置 i+δ处的位置编码可以线性投影位置i处的位置编码来表示。

13 计算机视觉

13-1 图像增强

大型数据集是成功应用深度神经网络的先决条件，图像增广是对训练图像进行一系列的随机变化后，生成相似但不相同的训练样本，从而扩大训练集的规模。此外，应用图像增广的原因是：随机改变训练样本可以减少模型对某些属性的依赖，从而提升泛化性能。
通过从后向前推，确定使用什么样的数据增强，也就是测试集的图像和训练集的图像有什么不同

13-1-1 常用的图像增强方法

翻转和裁切
左右翻转通常不会改变图像的类别，使用 transforms 模块来创建 RandomFlipLeftRight 实例，这样就会各有 50%的概率使得图像向左或者向右翻转
其中上下翻转是：RandomFlipTopBottom
通过池化层, 可以降低对位置的敏感度, 通过对图像进行随机裁剪，使物体以不同的比例出现在图像的不同位置。这也可以降低模型对目标位置的敏感性
下面的代码将随机裁剪一个面积为原始面积10%到100%的区域，该区域的宽高比从0.5～2之间随机取值。然后，区域的宽度和高度都被缩放到200像素

torchvision.transforms.RandomResizedCrop(
    (200, 200), scale=(0.1, 1), ratio=(0.5, 2))

改变颜色
可以改变图像颜色的四个方面：亮度、对比度、饱和度和色调
在下面的示例中，我们随机更改图像的亮度，随机值为原始图像的50% (0.5 到 1.5 之间)
其中, 亮度是 brightness, 对比度是 contrast, 饱和度是 saturation 色调是 hue

torchvision.transforms.ColorJitter(
    brightness=0.5, contrast=0, saturation=0, hue=0)

多种方式同时使用
使用 torchvision.transforms.Compose() 把上述方法结合起来

13-2 微调

为了实现对图片的识别，可以自己收集数据集，但是费用太贵，也可以使用再 ImageNet 上的图片，适用于 ImageNet 的复杂模型可能会过拟合，此外，由于训练样本数量有限，训练模型的准确性可能无法满足实际要求。
为了解决问题，可以使用迁移学习(transfer learning) 将源数据学到的知识迁移到目标数据集, 例如 Image 数据集中的大多数图像和椅子无关, 但在此数据集上训练的模型可能会提取更通用的图像特征, 这有助于识别边缘, 纹理, 形状和对象组合.这些类似的特征也可能有效的识别椅子

步骤
迁移学习中常见的技巧: 微调 fine-tuning
包括以下四个步骤:

在源数据集上预训练神经网络模型. 即源模型
创建一个新的神经网络模型, 即目标模型, 复制源模型的所有模型设计和参数(除了输出层).假定这些模型参数包含从源数据集中学到的知识, 这些知识也将适用于目标数据集, 还假设源模型的输出和源数据集的标签密切相关, 因此不在目标中使用该层
向目标模型中添加输出层, 输出数是目标训练集中的类别数, 然后随机初始化该层的模型参数(也可以重用分类器权重, 将预训练模型分类器中对应标号对应的向量来做初始化)
在目标数据集上训练目标模型, 输出层将从头开始训练, 而所有其他层的参数将根据源模型的参数进行微调(更强的正则化)

底层的特征更加通用, 可以固定住底层的参数

数据标准化

normalize = torchvision.transforms.Normalize(
    [0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
    # 这是在ImageNet随机抽样得来的

Normalize()函数的作用是将数据转换为标准高斯分布，即逐个channel的对图像进行标准化（均值变为 0 00，标准差为 1 11），可以加快模型的收敛，具体的采用

mean：各通道的均值
std：各通道的标准差
Inplace：是否原地操作
经常看到的 mean = [ 0.485 , 0.456 , 0.406 ] , std=[0.229, 0.224, 0.225]表示的是从 ImageNet数据集中随机抽样计算得到的

获取预训练模型
pretrained_net = torchvision.models.resnet18(pretrained=True)
替换并初始化输出层

finetune_net.fc = nn.Linear(finetune_net.fc.in_features, 2)
nn.init.xavier_uniform_(finetune_net.fc.weight);

对预训练层和最后输出层分别设置不同的学习率

trainer = torch.optim.SGD([{'params': params_1x},
                                   {'params': net.fc.parameters(),
                                    'lr': learning_rate * 10}],
                                lr=learning_rate, weight_decay=0.001)